What is a $q$-analog? (Part 1)
Hi, I’m Maria and I’m a $q$-analog addict. The theory of $q$-analogs is a little-known gem, and in this series of posts I’ll explain why they’re so awesome and addictive!
So what is a $q$-analog? It is one of those rare mathematical terms whose definition doesn’t really capture what it is about, but let’s start with the definition anyway:
Definition: A $q$-analog of a statement or expression $P$ is a statement or expression $P_q$, depending on $q$, such that setting $q=1$ in $P_q$ results in $P$.
So, for instance, $2q+3q^2$ is a $q$-analog of $5$, because if we plug in $q=1$ we get $5$.
Sometimes, if $P_q$ is not defined at $q=1$, we also say it’s a $q$-analog if $P$ can be recovered by taking the limit as $q$ approaches $1$. For instance, the expression \[\frac{q^5-1}{q-1}\] is another $q$-analog of $5$ - even though we get division by zero if we plug in $q=1$, we do have a well defined limit that we can calculate, for instance using L’Hospital’s Rule: \[\lim_{q\to 1} \frac{q^5-1}{q-1}=\lim_{q\to 1} \frac{5q^4}{1} = 5.\]
Now of course, there are an unlimited supply of $q$-analogs of the number $5$, but certain $q$-analogs are more important than others. When mathematicians talk about $q$-analogs, they are usually referring to ``good’’ or ``useful’’ $q$-analogs, which doesn’t have a widely accepted standard definition, but which I’ll attempt to define here:
More Accurate Definition: An interesting $q$-analog of a statement or expression $P$ is a statement or expression $P_q$ depending on $q$ such that:
- Setting $q=1$ or taking the limit as $q\to 1$ results in $P$,
- $P_q$ can be expressed in terms of (possibly infinite) sums or products of rational functions of $q$ over some field,
- $P_q$ gives us more refined information about something that $P$ describes, and
- $P_q$ has $P$-like properties.
Because of Property 2, most people would agree that $5^q$ is not an interesting $q$-analog of $5$, because usually we’re looking for polynomial-like things in $q$.
On the other hand, $\frac{q^5-1}{q-1}$, is an excellent $q$-analog of $5$ for a number of reasons. It certainly satisfies Property 2. It can also be easily generalized to give a $q$-analog of any real number: we can define \[(a)_q=\frac{q^a-1}{q-1},\] a $q$-analog of the number $a$.
In addition, for positive integers $n$, the expression simplifies: \[(n)_q=\frac{q^n-1}{q-1}=1+q+q^2+\cdots+q^{n-1}.\] So for instance, $(5)_q=1+q+q^2+q^3+q^4$, which is a natural $q$-analog of the basic fact that $5=1+1+1+1+1$. The powers of $q$ are just distinguishing each of our “counts” as we count to $5$. This polynomial also captures the fact that $5$ is prime, in a $q$-analog-y way: the polynomial $1+q+q^2+q^3+q^4$ cannot be factored into two smaller-degree polynomials with integer coefficients. So the $q$-number $(5)_q$ also satisfies Properties 3 and 4 above: it gives us more refined information about $5$-ness, by keeping track of the way we count to $5$, and behaves like $5$ in the sense that it can’t be factored into smaller $q$-analogs of integers.
But it doesn’t stop there. Properties 3 and 4 can be satisfied in all sorts of ways, and this $q$-number is even more interesting than we might expect. It comes up in finite geometry, analytic number theory, representation theory, and combinatorics. So much awesome mathematics is involved in the study of $q$-analogs that I’ll only cover one aspect of it today: $q$-analogs that appear in geometry over a finite field $\mathbb{F}_q$.
Counting lines in finite geometries
If you’ve ever played SET, you’ll know that it’s a fast-paced card game that some people are really annoyingly good at. But more interestingly, it’s based on the geometry of four-dimensional space over the finite field $\mathbb{F}_3$. Each card in SET has four attributes: color, shape, number, and shading, which can be thought of as the $x$, $y$, $z$, and $t$ axes in a four dimensional space. Then, each of these attributes has 3 possible values, so we can think of them as numbers modulo $3$, or more rigorously, elements of the finite field $\mathbb{F}_3$. So a card in SET is a point in $\mathbb{F}_3^4$, which looks like a $3\times 3\times 3\times 3$ grid of points. The ``sets’’ in SET are then ``lines’’ in this finite geometry!
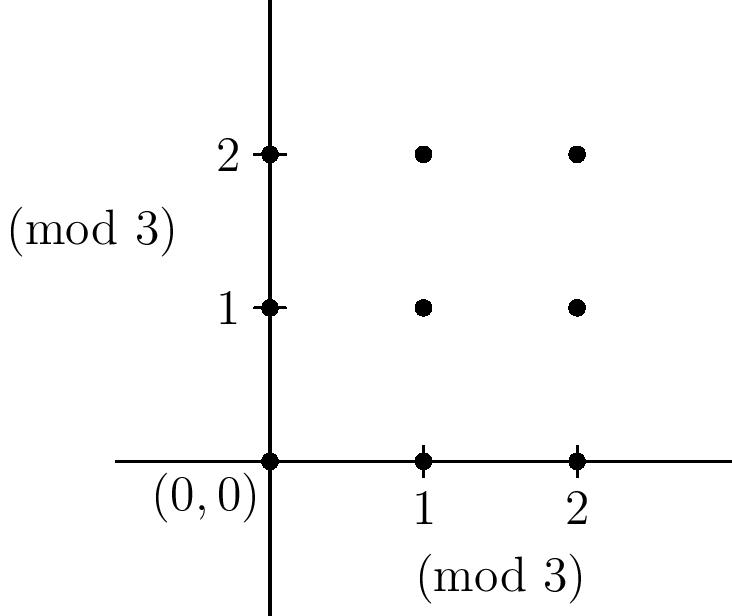
It’s hard to imagine four dimensional grids, though, so let’s consider the finite plane $\mathbb{F}_3^2$, which looks like this:
A line can be defined like lines in the usual plane: the solution set to a linear equation $ax+by=c$, where all variables are assumed to have variables in $\mathbb{F}_3^4$. So for instance, the line $x+y=0$ consists of the points $(0,0)$, $(1,2)$, and $(2,1)$ above. It certainly doesn’t look like those three points form a ``line’’, but remember, we’re taking everything modulo $3$ and so the geometry is bound to look a bit different.
How many lines are there in $\mathbb{F}_3^2$? Well, let’s first count the lines passing through $(0,0)$, which must be defined by equations of the form $ax+by=0$. It is still true in this finite geometry that there is a unique line passing through any two points (can you see why?), and there are $3^2-1$ points other than $(0,0)$ that we can choose as the second point on the line. So our answer must be $8$, right?
Wrong! We double-counted - for instance, the line $(0,0),(1,2),(2,1)$ was counted once by choosing $(1,2)$ as the second point, and again by choosing $(2,1)$. Since each line contains three points (can you see why?), we overcounted each line $3-1$ times. So, the number of lines through $(0,0)$ is $\frac{3^2-1}{3-1}=4$.
To count all lines, then, for each equation of the form $ax+by=0$, there are two more of the form $ax+by=1$ and $ax+by=2$ which do not pass through $(0,0)$. Thus, there are three times as many lines total as those that pass through the origin. Our total is $4\cdot 3=12$.
By the same argument, in $\mathbb{F}_q^n$, we’d have $q^n-1$ ways to choose a point other than the origin, which overcounts the lines through the origin $q-1$ times each. So there are $\frac{q^n-1}{q-1}$ lines through the origin, and $q\frac{q^n-1}{q-1}$ lines total. Look familiar?
Indeed, we’ve stumbled across our $q$-analog of $n$, in sort of an odd place: the geometry over a finite field $\mathbb{F}_q$ where $q=p^r$ is a power of a prime. This is rather strange because there is no finite field of order $1$, and yet somehow we are supposed to set $q=1$ to determine that this is, indeed, a $q$-analog of something. In fact, there is a theory of geometry over the finite field of order $1$, even though such a field cannot exist! The theory turns out to reduce to basic combinatorics of sets, and the link between the two is summarized nicely here.
Counting subspaces
What if we now try to count $k$-dimensional subspaces, like planes or hyperplanes, rather than lines through the origin? It turns out that the easier place to start is to count the flags in $\mathbb{F}_q^n$, that is, the chains of subspaces \[0=F_0\subset F_1\subset F_2 \subset \cdots \subset F_n=\mathbb{F}_q^n\] of subspaces where $\dim F_i=i$ for all $i$. The space $F_0$ must be $0$, and there are $(n)_q=\frac{q^n-1}{q-1}$ ways to choose the subspace $F_1$. Now, each $2$-dimensional subspace $F_2$ containing $F_1$ corresponds to a unique line in the $n-1$-dimensional quotient space $\mathbb{F}_q^n/F_1$, which gives $(n-1)_q$ possibilities for $F_2$. Continuing in this fashion, there are \[(n)_q(n-1)_q(n-2)_q\cdots (2)_q(1)_q\] flags. We call this the $q$-factorial, and is often written $(n)_q!$. We explored the combinatorics of this polynomial in this post and this one, and from this it’s clear that the $q$-factorial gives a natural combinatorial analog of the fact that there are $n!$ permutations of $1,\ldots,n$. It gives us a more refined count of permutations, according to how ``mixed up’’ they are.
Finally, we can count the number of $k$-dimensional subspaces $F_k$ as follows. Any such subspace $F_k$ can be extended to form a complete flag, and there are $(k)_q!$ ways of forming the subspaces contained in $F_k$, and $(n-k)_q!$ ways of forming the larger subspaces containing $F_k$. Since there are $(n)_q!$ flags total, and each $F_k$ appears $(k)_q!(n-k)_q!$ times in this count, we have that there are \[\frac{(n)_q!}{(k)_q!(n-k)_q!}\] $k$-dimensional subspaces of $\mathbb{F}_q^n$. This expression is a natural $q$-analog of the binomial coefficient $\binom{n}{q}=\frac{n!}{k!(n-k)!}$.
This $q$-binomial coefficient appears everywhere, and we’ll continue exploring its properties next week!