Moduli of Curves IV: Getting classy
Young tableaux are to planes as labeled trees are to curves. Continuing from the previous post in this series, we introduce the Chow ring of $\overline{M}_{0,n}$ and some important classes.
Recall that in the first post, we answered the question “How many cubic curves in $\mathbb{P}^3$ pass through $5$ general points and are tangent to a given general plane at each of two of the points?” The answer was $2$, and the key to answering questions such as these is to work in the Chow ring of the moduli space.
Roughly speaking, the Chow ring will consist of equivalence classes of subvarieties of the moduli space, and give us ways to answer generic intersection problems. In the above problem, the closed subvarieties in consideration will be the set of all curves passing through the 5 points and tangent to just one of the planes, which corresponds to the psi classes $\psi_1$ and $\psi_2$. Then, multiplying classes in the Chow ring corresponds to intersections of (appropriately chosen representatives of) the corresponding subvarieties, and we have turned our intersection problem into a multiplication problem in a ring.
Read on below…
Moduli of Curves III: Gaining perspective
Young tableaux are to planes as labeled trees are to curves. Continuing from the previous post in this series, we now show how to think of $\overline{M}_{0,n}$ as a projective variety.
We now show how to look from the perspective of a single point, and combine this with the forgetting maps, to construct a projective embedding of $\overline{M}_{0,n}$ and thereby realize it as a geometric space itself, rather than just as a set of curves. The key new construction we need is the Kapranov map.
The Kapranov map
Given a curve $C\in \overline{M}_{0,n}$, consider the $\mathbb{P}^1$ component that the marked point $n$ is on. The other special points on this component are either nodes, each leading to a distinct branch of the dual tree, or marked points (which can be considered branches with just one leaf). Choose coordinates on this $\mathbb{P}^1$ in a way so that point $n$ is at coordinate $\infty=(1:0)$, and the branch containing marked point $1$ is attached at coordinate $0=(0:1)$. Then define the Kapranov map \[ \psi_n: \overline{M}_{0,n}\to \mathbb{P}^{n-3} \] that sends a curve $C$ to the tuple $(x_2:x_3:\cdots : x_{n-1})$ where $(x_i:1)$ is the coordinate at which the branch containing $i$ is attached to $n$’s component. (Note that this means that all $x_i$’s for $i$ in a given branch are equal.)
Moduli of Curves II: I forgot my point!
Young tableaux are to planes as labeled trees are to curves. Continuing from the motivation of the previous post, we now dive into the structure of the moduli space $\overline{M}_{0,n}$, and construct two recursive structures that lead to beautiful inductive theory, and, in the next post, the construction of the space as a projective variety.
Let’s start with a definition of the noncompact interior $M_{0,n}$, also described in this combinatorial post on enumeration of trivalent trees.
Definition. The moduli space $M_{0,n}$, as a set, is the set of all isomorphism classes of choices of $n\ge 3$ distinct points $p_1,\ldots,p_n$ on the projective line $\mathbb{P}^1$, up to projective isomorphism.
Note that the $0$ in $M_{0,n}$ means “genus $0$”, as in, we are not choosing points on a torus, but on a genus $0$ Riemann surface.
Moduli of Curves I: A Curious Curve Count
Young tableaux are to planes as labeled trees are to curves. This is the analogy from which I hope to start a series of posts on the beauty of the growing field of connections between the geometry of moduli spaces of curves, and combinatorics.
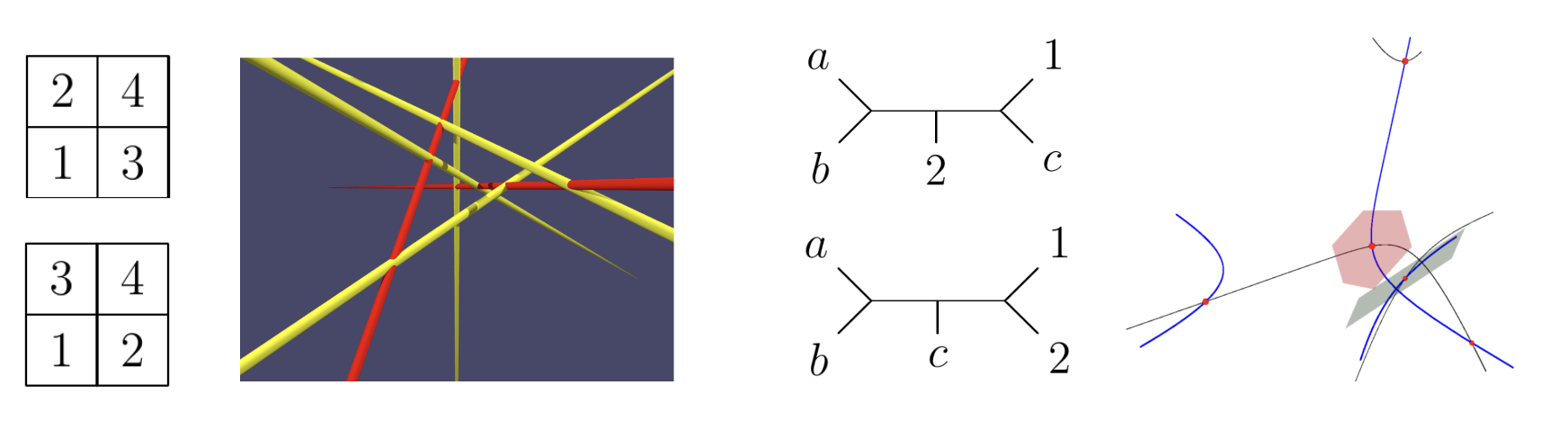
What do the pictures above have in common?
Sum of squares of chords to the points of a regular $n$-gon
The CSU math graduate students have started writing a really fun monthly math magazine for the department, featuring stories, mathematical tidbits, and puzzles collected from the department and slid under all the professors’ doors each month. It’s been a joy to read, and every month they have a “Problem of the Month’’ as well. This month’s problem was particularly fun:
Let $P_1,P_2,\ldots,P_n$ be $n\ge 2$ points equally spaced around a circle of radius $r$, forming a regular $n$-gon. Let $X$ be any random point on the circle. Show that \(\|XP\_1\|^2+\|XP\_2\|^2+\\\cdots +\|XP\_n\|^2 = 2nr^2.\)
It’s fun to first prove this for $n=2$. In this case, the two chords $XP_1$ and $XP_2$ form a right angle because $P_1P_2$ is a diameter of the circle (and the angle spanning ). So by the Pythagorean theorem the sum of their squares is the square of the hypothenuse (diameter), which $(2r)^2=4r^2$, as desired:
How would you approach this? Here is a clean solution using complex numbers: