The Mad Veterinarian

I volunteered at the Julia Robinson Math Festival held at a nearby school last Saturday. It was a great event for kids in 4th to 9th grade in the area, featuring a room full of mathematical activity tables and raffle tickets to be given out as rewards for a good idea or explanation.

The table I was working at featured a number of problems about a ``mad veterinarian’’. He had a machine that you can feed two cats to and get a dog out. You can also feed it two dogs to get one dog out, and if you feed it a cat and a dog, you get out a cat. The veterinarian wants to end up with only one cat, and no other animals. Can he do this starting with three cats and one dog? How about four cats and two dogs?

Rota's Indiscrete Thoughts

I am a huge fan of Gian-Carlo Rota, who has been said to be the founding father of modern algebraic combinatorics. (He is also my mathematical grandfather-to-be.)

Rota was a philosopher as well as a mathematician, and wrote an entire book primarily concerning the philosophy of mathematics. His book is called Indiscrete Thoughts.

Knuth equivalence on a necklace

Lately, I’ve been working on some open problems related to a Young tableau operation called catabolism, which involves some interesting tableaux combinatorics. While working the other day, I encountered a simple and beautiful fact that I never would have expected.

Suppose we have a word $w$ whose letters are from the alphabet $\{1,\ldots,n\}$ (allowing repeated letters). A Knuth move is one of the following:

1. Given three consecutive letters $xyz$ with $x>y$ and $x\le z$, replace $xyz$ with $xzy$, or vice versa (replace $xzy$ with $xyz$).

2. Given three consecutive letters $xyz$ with $z\ge y$ and $z\lt x$, replace $xyz$ with $yxz$, or vice versa (replace $yxz$ with $xyz$).

In other words, if you have three consecutive letters and either the first or the third lies between the other two in size, the end letter acts as a pivot about which the other two letters switch places. Visually:

Yet another definition of the Schur functions

I continue to be amazed at the multitude of different contexts in which the Schur functions naturally appear.

In a previous post, I defined the Schur symmetric functions combinatorially, via the formula \[s_\lambda=\sum_{|\mu|=|\lambda|}K_{\lambda\mu} m_\mu\] where $K_{\lambda\mu}$ is the number of semistandard Young tableaux of shape $\lambda$ and content $\mu$ and $m_\mu$ is the monomial symmetric function of shape $\lambda$. I also defined them as the ratio \[s_\lambda=\frac{a_{\lambda+\delta}}{a_\lambda}\] where $a_\lambda$ is the elementary antisymmetric function.

And, in another post, I pointed out that the Frobenius map sends the irreducible characters of the symmetric group $S_n$ to the Schur functions $s_\lambda$. This can be taken as a definition of the Schur functions:

Early Easter Egg

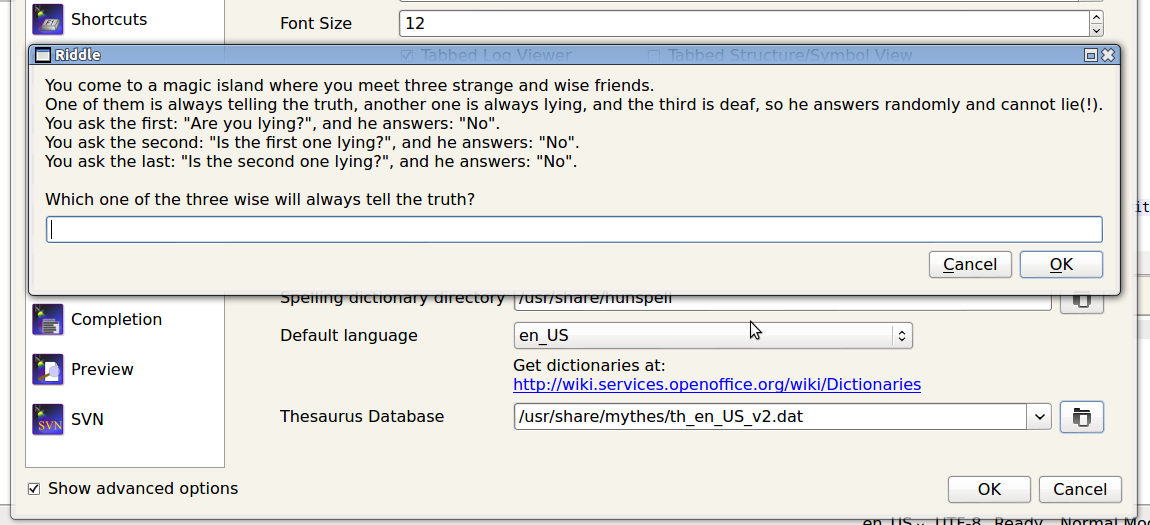
It’s not springtime just yet, but I found myself nerd sniped this week by an easter egg in my favorite LaTeX editor, TeXStudio.

I had to reinstall it recently, and my customized advanced configurations were set back to the defaults. So I opened the Options -> Configure TeXStudio menu, and tried to click on the “Show advanced options” checkbox. This is what popped up:

That’s right, a “Riddle” window popped up with the following problem: