Yet another definition of the Schur functions

I continue to be amazed at the multitude of different contexts in which the Schur functions naturally appear.

In a previous post, I defined the Schur symmetric functions combinatorially, via the formula \[s_\lambda=\sum_{|\mu|=|\lambda|}K_{\lambda\mu} m_\mu\] where $K_{\lambda\mu}$ is the number of semistandard Young tableaux of shape $\lambda$ and content $\mu$ and $m_\mu$ is the monomial symmetric function of shape $\lambda$. I also defined them as the ratio \[s_\lambda=\frac{a_{\lambda+\delta}}{a_\lambda}\] where $a_\lambda$ is the elementary antisymmetric function.

And, in another post, I pointed out that the Frobenius map sends the irreducible characters of the symmetric group $S_n$ to the Schur functions $s_\lambda$. This can be taken as a definition of the Schur functions:

The Schur functions $s_\lambda$, for $|\lambda|=n$, are the images of the irreducible representations of $S_n$ under the Frobenius map.

Today, I’d like to introduce an equally natural representation-theoretic definition of the Schur functions:

The Schur functions $s_\lambda$, for $\lambda$ having at most $n$ parts, are the characters of the polynomial representations of the general linear group $GL_n(\mathbb{C})$.

I recently read about this in Fulton’s book on Young Tableaux, while preparing to give a talk on symmetric function theory in this term’s new seminar on Macdonald polynomials. Here is a summary of the basic ideas:

A polynomial representation of $GL_n(\mathbb{C})$ is a homomorphism to $GL_m(\mathbb{C})$ for some $m$ such that each coordinate function is a polynomial function of the $n^2$ entries of the original matrices. For instance, the determinant representation, which sends each matrix \[X=\left(x_{ij}\right)_{i,j=1}^n\] to the $1\times 1$ matrix \[\left(\det(X)\right)\] is a polynomial representation because the determinant is a polynomial in the variables $x_{ij}$.

The character of a polynomial representation, then, is defined to be the trace of the action of the diagonal matrix \[\left(\begin{array}{cccc} x_1 & 0 & \cdots & 0 \\ 0 & x_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & x_n \end{array}\right).\] That is, the character is the trace of the image of this matrix in $GL_m$, which must be a polynomial in the variables $x_1,\ldots,x_n$. Magically, these turn out to be the Schur functions in the case of the irreducible representations of $GL_n$.

The irreducible polynomial representations of $GL_n$ can be constructed in several ways. One is an explicit construction similar to that of the Specht module construction for the irreducible representations of $S_n$. The modules in the case of $GL_n(\mathbb{C})$ are called Schur modules, and they can be defined as follows.

First, let $V=\mathbb{C}^n$ be the standard representation of $GL_n$, and consider the induced $GL_n$-module \[\Lambda^{\lambda_1^\ast}V\otimes \Lambda^{\lambda_2^\ast}V \otimes \cdots \otimes \Lambda^{\lambda_l^\ast}V,\] where $\lambda^\ast$ is the conjugate partition of $\lambda$ and has $l$ rows. We can think of this as the space of Young tableaux $T$ of shape $\lambda$ with entries in $V$, such that, if $T’$ is formed from $T$ by interchanging two elements of the same column, then $T=-T’$.

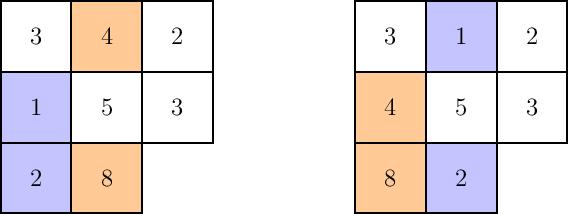
Given a Young tableau of shape $\lambda$ whose box labels are elements of $V$, a column exchange is given by choosing two columns, choosing $k$ entries from each column for some $k$, and interchanging them, preserving their vertical ordering. For instance, we show below a transfer of two entries chosen from each of the first and second columns:

Finally, define the Schur module $V^\lambda$ to be the quotient \[V^\lambda=\Lambda^{\lambda_1^\ast}V\otimes \Lambda^{\lambda_2^\ast}V \otimes \cdots \otimes \Lambda^{\lambda_l^\ast}V/Q,\] where $Q$ is the submodule generated by the relations $T-\sum U$, where $U$ ranges over the tableaux formed from $T$ by all possible exchanges between two fixed columns in $T$, where the boxes on the right column are fixed as well. Then this module $V^\lambda$, and all other such modules, turn out to be precisely the irreducible polynomial representations of $GL_n$!

It takes some work to prove this and show that the Schur functions are their characters. Nevertheless, I feel that this particular construction of the Schur modules $V^\lambda$ gives insight into how the Schur functions are related, given their combinatorial definition in terms of tableaux.