The Springer Correspondence, Part II: The Resolution

This is a continuation of The Springer Correspondence, Part I. Here we will work with unipotent matrices to construct the Springer resolution and the cohomology of its fibers.

Unipotent Matrices and Partitions

A unipotent element of a linear algebraic group $G$ is any element $u\in G$ such that $1-u$ is nilpotent. That is, $u=1+n$ where $n^k=0$ for some $k$.

To get a sense of what unipotent matrices look like, consider the type A situation in which $\DeclareMathOperator{\GL}{GL}\newcommand{\CC}{\mathbb{C}} G=\GL_n(\CC)$. Given a unipotent element $u$, we can conjugate it by some matrix to put it in Jordan normal form. It will look something like this: \[gug^{-1}=\left(\begin{array}{ccccccc} \lambda_1 & 1 & & & & & \\ & \lambda_1 & 1 & & & & \\ & & \lambda_1 & & & & \\ & & & \lambda_2 & 1 & & \\ & & & & \lambda_2 & & \\ & & & & & \ddots & \\ & & & & & & \lambda_k \end{array}\right)\]

It turns out that the matrix above is particularly simple in this case:

The eigenvalues $\lambda_i$ of a unipotent matrix are all $1$.

To see this, suppose $\lambda$ is an eigenvalue of $u$. We have $uv=\lambda v$ for some vector $v$, and so \[(1-u)v=(1-\lambda)v.\] Since $1-u=n$ is nilpotent, say with $n^k=0$, we have \[(1-u)^kv=(1-\lambda)^kv=0,\] so $(1-\lambda)^k=0$. Since $\lambda\in\CC$ and $\CC$ is a field, it follows that $\lambda=1$, as claimed.

Therefore, every unipotent matrix is conjugate to a matrix havnig all $1$’s on the diagonal, $0$’s or $1$’s on the off-diagonal, and $0$’s everywhere else. The blocks of $1$’s on the off-diagonal split the matrix into Jordan blocks, which we can order by size from greatest to least. Let the sizes of the Jordan blocks be $\mu_1,\mu_2,\ldots,\mu_k$. Then $\mu=(\mu_1,\ldots,\mu_k)$ is a partition of $n$, and determines the conjugacy class of a given unipotent matrix.

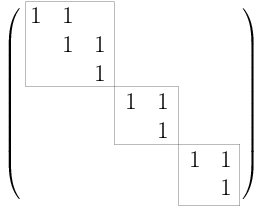
For instance, the partition $\mu=(3,2,2)$ corresponds to the conjugacy class of unipotent matrices with the Jordan canonical form below.

This can all be summed up in the following fact:

The unipotent conjugacy classes in $\GL_n$ are in one-to-one correspondence with the partitions of $n$.

Now, I know what you are thinking:

“Maria, if the unipotent conjugacy classes of $\GL_n$ and the irreducible representations of $S_n$ are both indexed by the partitions of $n$, shouldn’t there be some nice geometric construction that relates them directly?”

Indeed there is! The Springer correspondence gives just that - and furthermore relates the unipotent conjgacy classes of any Lie group $G$ to the representations of its Weyl group.

The Springer Resolution

In what follows, let $G$ be a Lie group, and let $U$ be the subvariety of $G$ consisting of all unipotent elements. The variety $U$ is not smooth in general, and to resolve the singularities we construct the variety $\widetilde{U}\subset U\times \mathcal{B}$ by \[\widetilde{U}=\{(u,B):u\in B\}.\] Recall from the previous post that $\mathcal{B}$ is the variety of all Borel subgroups of $G$ and is isomorphic to the Flag variety $G/B$ for any Borel $B$. If we interpret $\mathcal{B}$ as the Flag variety in the case $G=\GL_n$, we can alternatively define $\widetilde{U}$ as the set of all pairs $(u,F)$ where $F$ is a flag and $u$ fixes $F$, that is, $uF_i=F_i$ for each $i$.

It turns out that $\widetilde{U}$ is smooth and the projection map \[\pi:\widetilde{U}\to U\] is proper, so it resolves the singularities in $U$. This map is known as the Springer resolution.

The theory gets rather deep at this point, so in what follows I will state the main facts without proof. For full details I refer the interested reader to the exposition in Chapter 3 of Representation Theory and Complex Geometry by Chriss and Ginzburg.

Springer Fibers and Weyl Group Action

For any $x\in U$, define the Springer fiber $\mathcal{B}_x$ to be the fiber $\pi^{-1}(x)$ of the Springer resolution over $x$, that is, the set of all Borel subgroups of $G$ that contain $x$. Now, consider the cohomology ring $H^\ast(\mathcal{B}_x)$ over $\CC$. It turns out that there is an action of the Weyl group $W$ on this cohomology ring, called the Springer action.

There is unfortunately no direct way of defining this action. To get some intuition for where the action comes from, notice that the Springer resolution above can be lifted to the entire group: one can define $\widetilde{G}$ to be the subvariety of $G\times \mathcal{B}$ consisting of all pairs $(g,B)$ such that $g\in B$. Now, let $x$ be a regular semisimple element of $G$.

In the case $G=\GL_n$, a regular semisimple element is simply a diagonalizable element $x$ with $n$ distinct nonzero eigenvalues. If $x$ is of this form, any subspace of $\CC^n$ fixed by $x$ is a direct sum of its (linear) eigenspaces. So, if $V_1,\ldots,V_n$ are the eigenspaces corresponding to the distinct eigenvalues of $x$, any flag fixed by $x$ is of the form \[V_{\sigma(1)}\subset V_{\sigma(1)}\oplus V_{\sigma(2)}\subset \cdots \subset V_{\sigma(1)}\oplus \cdots \oplus V_{\sigma(n)}\] for some permutation $\sigma$ of $\{1,2,\ldots,n\}$. It follows that $\mathcal{B}_x$ consists of exactly $n!$ flags, and has a natural action of $S_n$ via permuting the eigenspaces $V_i$. Therefore, $S_n$ acts on $\mathcal{B}_x$ and therefore on $H^\ast(\mathcal{B}_x)$.

In general, if $x$ is regular and semisimple, the fiber $\mathcal{B}_x$ is a finite set of size $|W|$ where $W$ is the Weyl group of $G$. The regular semisimple elements form a dense subset of $G$, and one can use this to extend the action to all cohomology rings $H^\ast(\mathcal{B}_x)$ for any $x\in G$. This is the tricky part, and involves many more constructions than fit in a reasonable-length blog post, so again I refer the reader to this awesome book.

The Springer Correspondence

We’re finally ready to state the Springer correspodence. For $x\in G$, let $d(x)$ be the dimension of the Springer fiber $\mathcal{B}_x$.

In the case $G=\GL_n$, the top cohomology groups $H^{d(x)}(\mathcal{B}_x)$ are $S_n$-modules due to the Springer action described above. Notice also that $\mathcal{B}_x$ depends only on the conjugacy class of $x$, so for $x$ in the unipotent conjugacy class with shape $\mu$, we write $\mathcal{B}_\mu$ to denote this Springer fiber, with $d(\mu)$ its dimension. It turns out that these $S_n$-modules are precisely the irreducible representations of $S_n$.

The $S_n$-module $H^{d(\mu)}(\mathcal{B}_\mu)$ is isomoprhic to the irreducible representation $V_\mu$ of $S_n$ corresponding to $\mu$.

And there you have it.

For general Lie groups $G$, the Springer correspondence is not quite as nice; the top cohomology groups $H^d(\mathcal{B}_u)$ (where $u$ is a unipotent conjugacy class) are not in general irreducible $W$-modules. However, all of the irreducible $W$-modules occur exactly once as a summand among the modules $H^d(\mathcal{B}_u)$, and there is a correspondence between the irreducible representations of $W$ and pairs $(u,\xi)$ where $u$ is a unipotent conjugacy class in $G$ and $\xi$ is an irreducible $G$-equivariant local system on $u$.

Hall-Littlewood Polynomials

The fact that the top cohomology groups $H^{d(\mu)}(\mathcal{B}_\mu)$ are so nice naturally raises the question: what about the other cohomology groups? What $S_n$-modules do we get in each degree?

In particular, let $R_\mu=H^\ast(\mathcal{B}_\mu)$. Then $R_\mu$ is a graded $S_n$-module with grading \[R_\mu=\bigoplus (R_\mu)_i=\bigoplus H^i(\mathcal{B}_\mu),\] and so we can construct the Frobenius series \[F_t(R_\mu)=\sum_{i=0}^{d(\mu)}F((R_{\mu})_i)t^i\] where $F$ is the Frobenius map that sends $S_n$-modules to symmetric functions.

The Hall-Littlewood polynomials $\widetilde{H}_\mu(\mathbf{x};t)$ are defined to be the Frobenius characteristics $F_t(R_\mu)$, and are therefore a class of symmetric polynomials in the variables $\mathbf{x}=x_1,x_2,\ldots$ with coefficients in $\mathbb{Q}[t]$. They have incredibly rich combinatorial structure which reveals the decomposition of $R_\mu$ into irreducible $S_n$-modules… structure that I will save for a later post. Stay tuned!