Can you prove it?

As this ingenious post over at Math With Bad Drawings explained so clearly recently, there is a big difference between finding the answer to a math problem and being able to explain, beyond all reasonable doubt, why your answer is correct. It is the difference between solving it and proving it!

While mathematical proof is a huge part of math and science, it is unfortunately somewhat overlooked in the standard US curriculum. Partly for this reason, my family and I started a new math summer camp called Prove it! Math Academy. This year’s program will be a two-week crash course in proofs, using challenging problems and advanced mathematical concepts as examples.

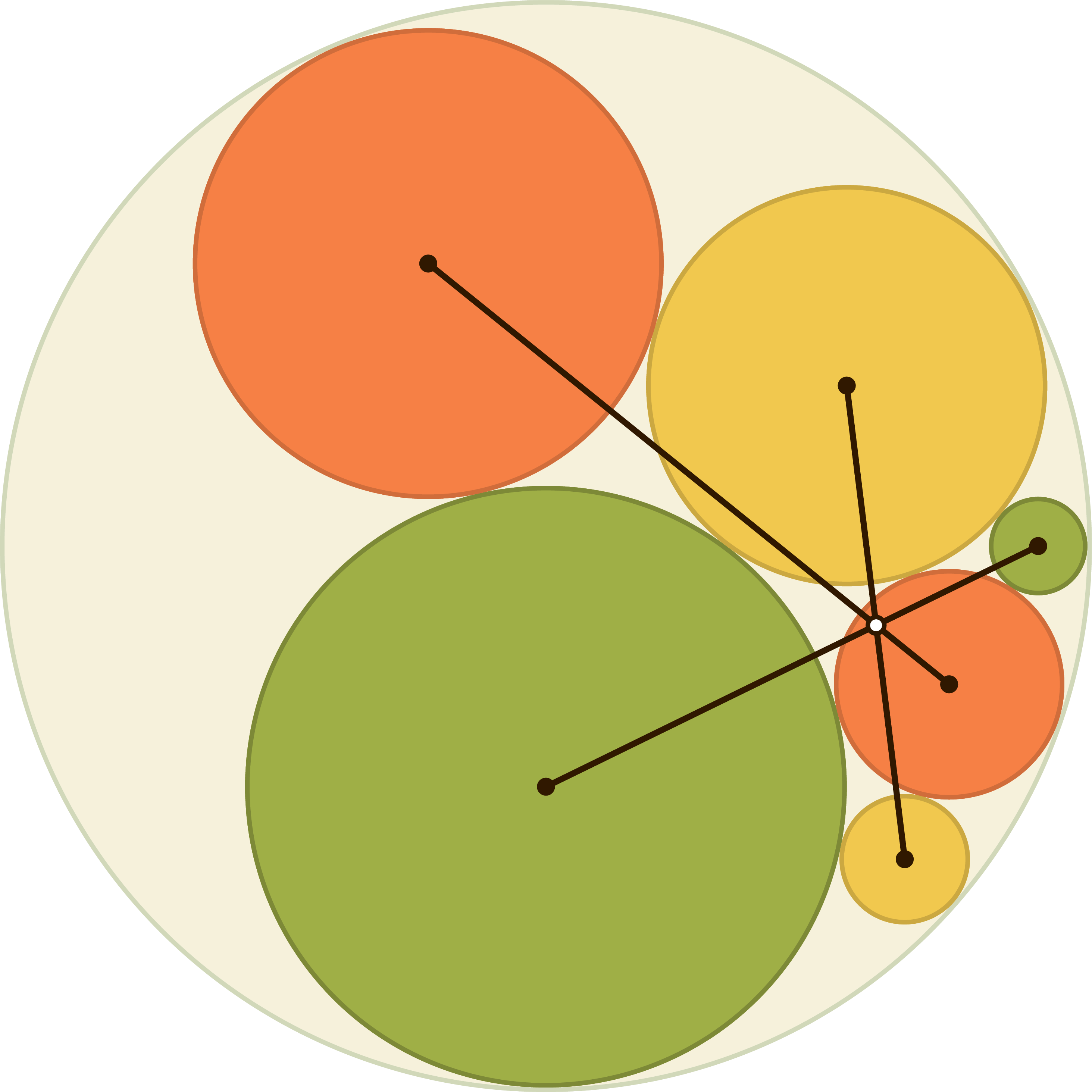
Consider the following diagram which appears on our program website:

No explanation, no words, no proof. Just the picture. Enticing!

The first step in proving a fact is to state exactly what it is you are trying to prove. In this case, one might generalize/interpret this diagram as follows. Suppose you have a circle $O$ (the big white one) containing three circles $A$, $B$, and $C$ inside of it that are mutually externally tangent to each other and internally tangent to $O$. (These three circles $A$, $B$, and $C$ would be the large green, large yellow, and small red circle in the diagram above.) Now let $X$, $Y$, and $Z$ be the remaining green, yellow, and red circles respectively: for instance, $X$ is the circle tangent internally to $O$ and externally to $B$ and $C$. Then the lines $AX$, $BY$, and $CZ$ connecting the centers of these circles all meet at one point - they are concurrent.

You can construct this in Geogebra or Asymptote. You can vary the sizes of the circles and test that indeed, these lines always seem to be concurrent. But unlike in science, lots of evidence to support a fact is not good enough in mathematics. We want to prove beyond all reasonable doubt that this is always true, no matter what the sizes of the circles are. In other words, you can solve it, but can you prove it?

A very elegant solution to this problem, which appears on the next page of this post, is due to Michael Kural, one of my former students at MOP. He was intrigued by the image on our program flyer at a recent math tournament, and came up with a proof using only Desargues’ theorem, Monge’s theorem, homothety, and inversion. Read on!

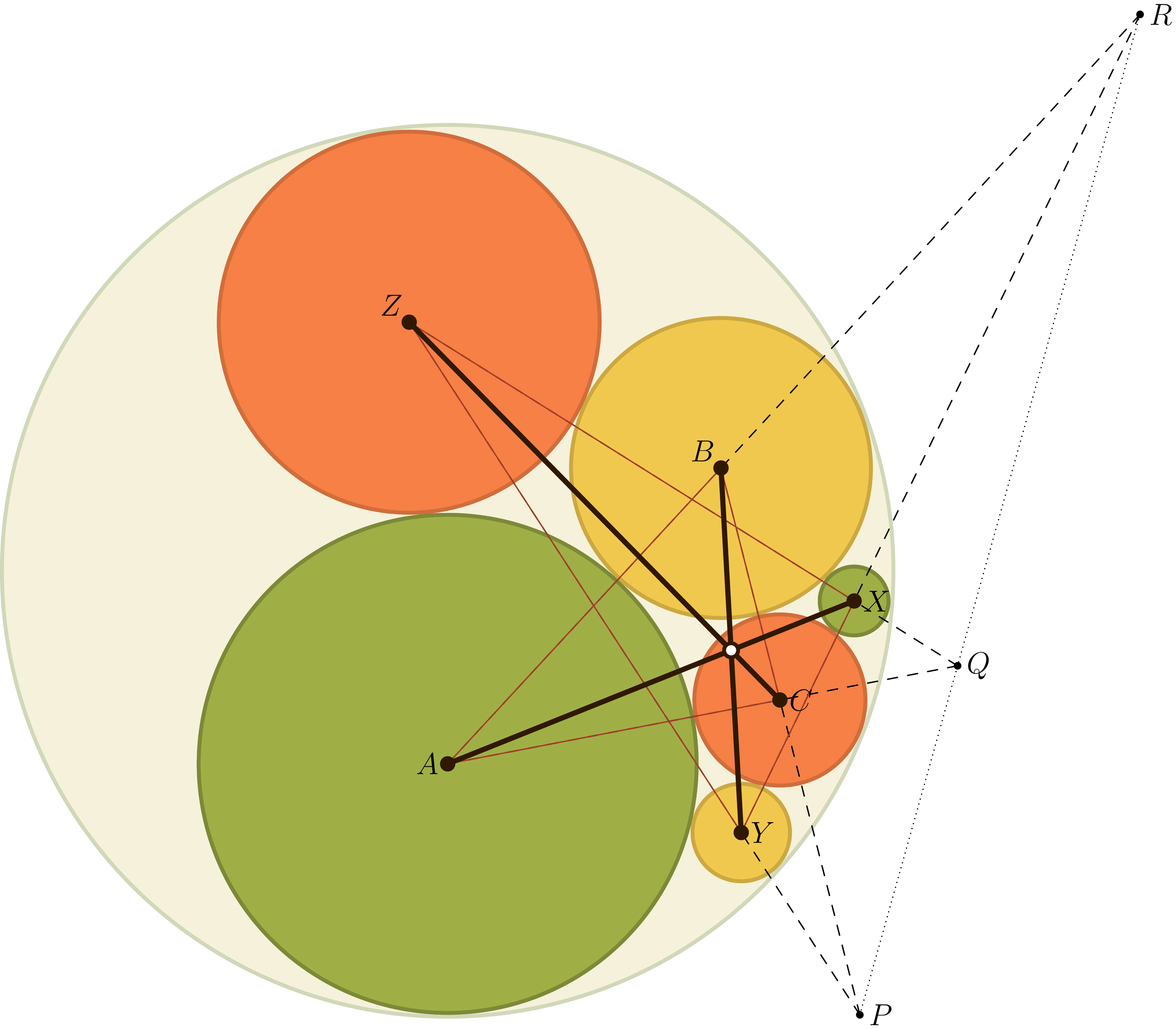
We wish to show that the lines $AX$, $BY$, and $CZ$ concur at a point.

We can first use Desargues’ Theorem to change the concurrency problem into a collinearity problem. To show that the two triangles $ABC$ and $XYZ$ are perspective from a point, it suffices to show that they are perspective from a line. So, we wish to show that points $P=BC\cap YZ$, $Q=AC\cap XZ$, and $R=AB\cap XY$ are collinear, as shown below.

To show the collinearity, by Monge’s theorem it suffices to prove that $P$, $Q$, and $R$ are the centers of homothety sending circles $C$ to $B$, $C$ to $A$, and $B$ to $A$ respectively.

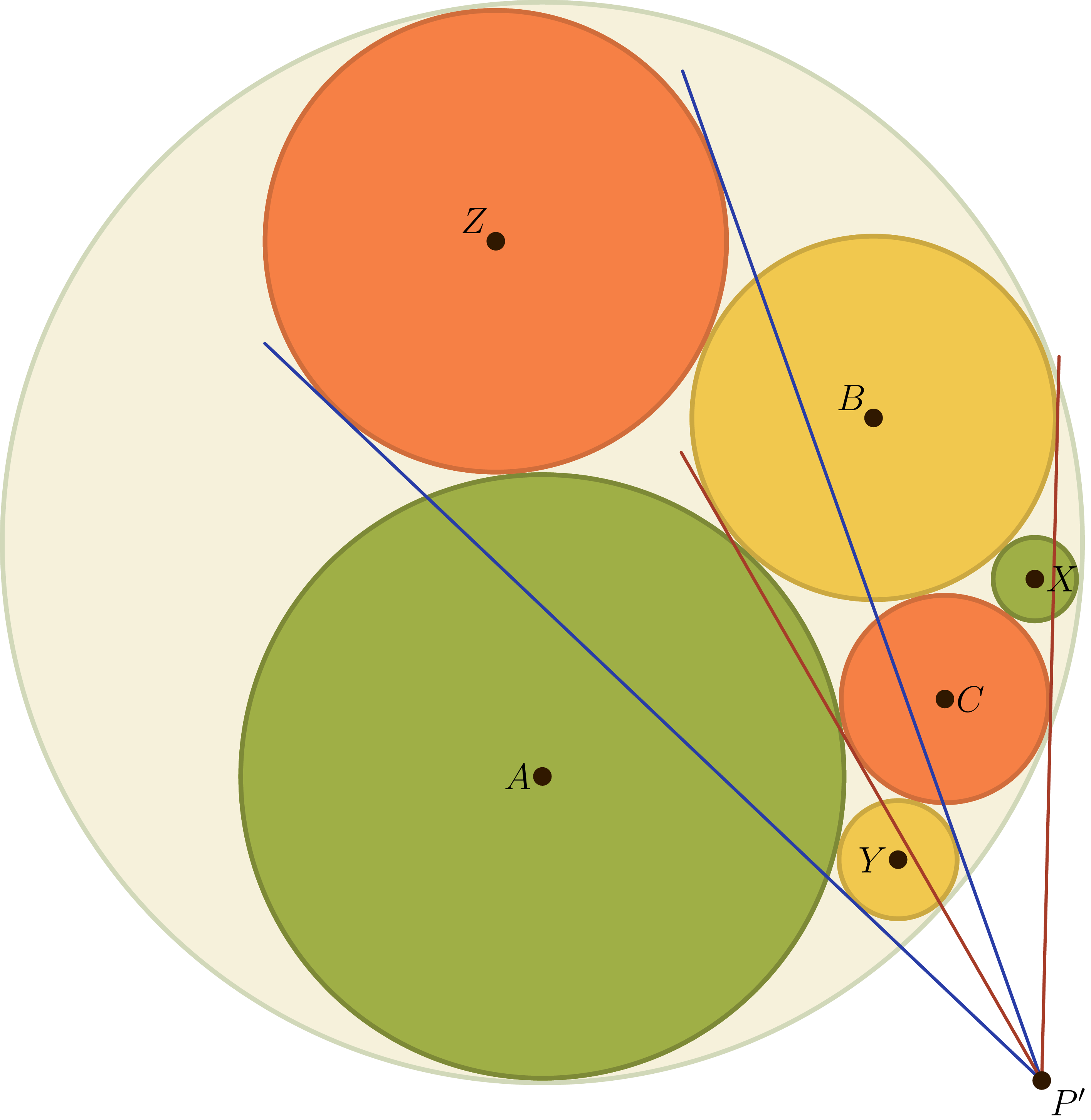
We claim that the center of homothety of circles $C$ and $B$ and that of circles $Y$ and $Z$ coincide. If they do, then they must coincide at $P$ since the lines joining the centers of these pairs pass through the centers of homothety. By symmetry, a similar fact will also hold for $Q$ and $R$, thereby satisfying the conditions of Monge’s theorem, and the proof will be complete.

So, it suffices to show that the center $P’$ of the homothety sending $C$ to $B$ is the same as the center of the homothety sending $Y$ to $Z$. Another way to say this is that the external tangents to $C$ and $B$ and those to $Y$ and $Z$ are concurrent at a point $P’$, as shown.

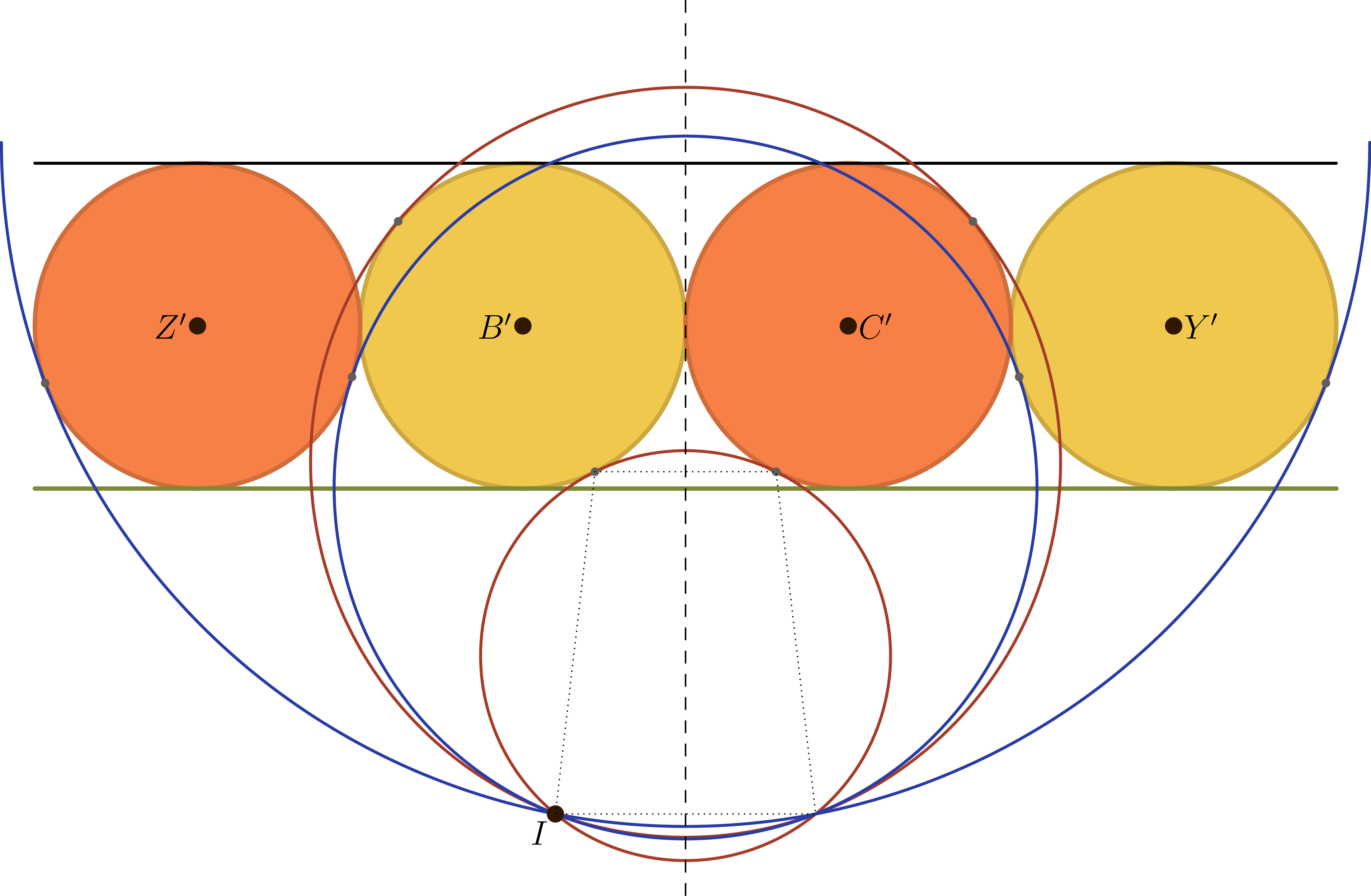
This claim can be shown using inversion. Specifically, let $I$ be the point of tangency of circle $A$ to the large circle $O$. If we invert the image above about any circle centered at $I$, the circles $A$ and $O$ are mapped to two parallel lines, and the four circles $B$, $C$, $Y$, and $Z$ are mapped to circles tangent to these two lines and tangent to each other in a row. The common external tangent lines to the pairs of circles are sent to circles passing through $I$ that are tangent to certain pairs of these circles:

Note that in the diagram above, the points $B’$, $Z’$, and so on do not refer to the images of the points $B$, $Z$, and so on under the inversion, but rather to the center of the images of their circles.

In the new diagram, the four circles $Z’$, $B’$, $Y’$, and $C’$ are congruent, and we can orient our picture so that the two parallel lines are horizontal. The two red circles passing through $I$ and tangent to $B’$ and $C’$ are therefore centered on the dashed vertical line of symmetry of the entire figure. It follows that the second intersection $P^{\prime\prime}$ of the two red circles is the reflection of $I$ about the vertical line. A similar argument shows that the two blue circles also intersect at the reflection of $I$ across the vertical line of symmetry. It follows that their intersections coincide at $P^{\prime\prime}$, as desired.