Higher specht polynomials

There are polynomials. There are Specht polynomials. And then there are higher Specht polynomials.

A colleague recently pointed out to me the results of this paper by Ariki, Terasoma, and Yamada, or more concisely summarized here. The authors give a basis of the ring of coinvariants \[R_n=\mathbb{C}[x_1,\ldots,x_n]/(e_1,\ldots,e_n)\] which, unlike the other bases we’ve discussed on this blog so far, respects the decomposition into irreducible $S_n$-modules. These basis elements include the ordinary Specht polynomials, but also some polynomials of higher degrees, hence the name ``higher’’ Specht polynomials.

Background: What is a Specht polynomial?

The construction of the irreducible representations of the symmetric group $S_n$ (called Specht modules) is often described in terms of ``polytabloids’’, but can be equivalently described in terms of a basis of Specht polynomials.

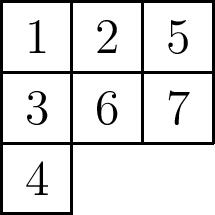
Before we describe this basis, recall that the dimension of the irreducible representation $V_\lambda$ of $S_n$ indexed by the partition $\lambda$ is equal to the number $f^\lambda$ of Standard Young Tableaux (SYT) of shape $\lambda$, i.e., the number of fillings of the Young diagram of $\lambda$ with the numbers $1,\ldots,n$ in such a way that the entries are increasing down rows and across columns. An example is shown below for $n=7$ and $\lambda=(3,3,1)$:

Given a standard Young tableau $T$, the Specht polynomial $F_T$ is defined as the following product taken over all of its columns $C$ \[F_T(x_1,\ldots,x_n)=\prod_{C} \prod_{i\lt j\in C}(x_j-x_i)\]

For instance, in the above tableau, \[F_T(x_1,\ldots,x_7)=(x_3-x_1)(x_4-x_1)(x_4-x_3)(x_6-x_2)(x_7-x_5).\]

In other words, the Specht polynomial for $T$ is the product of the Vandermonde determinants given by each of its columns’ entries. It is known that the set of polymomials $F_T$, where $T$ ranges over all SYT’s of shape $\lambda$, form a basis of their span, and their span is isomorphic to $V_\lambda$ as an $S_n$-module (here the $S_n$-action is the usual action on the variables $x_1,\ldots,x_n$).

Specht polynomials in the coinvariant ring

As described in detail in this post, the coinvariant ring is the $S_n$-module \[R_n=\mathbb{C}[x_1,\ldots,x_n]/(e_1,\ldots,e_n)\] where $e_i$ is the $i$th elementary symmetric function in the variables $x_1,\ldots,x_n$.

The ring $R_n$ inherits the action of $S_n$ on the polynomial ring, and we saw in the previous post on the coinvariant ring that it is isomorphic to the regular representation as an $S_n$-module. It is also graded by polynomial degree, with Hilbert series equal to $(n)_q!$. There are many known bases of $n!$ elements that respect this grading, but the ones we have described in previous posts do not respect the $S_n$-action. In particular, can we find an explicit basis which partitions into bases of the irreducible components in $R_n$?

To start, the Specht polynomials $F_T$ defined above are nonzero in $R_n$ and span one copy of each Specht module. But we know that in the regular representation, there are $f^\lambda$ copies of the irreducible representation $V_\lambda$ for each $\lambda$, and this construction only gives one copy of each. In fact, since the copies of $V_\lambda$ must be alternating in the column variables, they are the lowest-degree copies of each. Hence, we need higher Specht polynomials.

To define them, we first need to understand the RSK correspondence and the charge statistic.

The tools: RSK and charge

Somehow, in all of my years of blogging, I have never actually described the RSK (Robinson-Schensted-Knuth) correspondence. By the nature of the regular representation of $S_n$, we must have \[\sum_{\lambda \vdash n} (f^{\lambda})^2=n!\[ since each irreducible representation $V_\lambda$ of dimension $f^\lambda$ occurs exactly $f^{\lambda}$ times, and the regular representation has dimension $n!$. Recall also that $f^\lambda$ is the number of standard Young tableaux of shape $\lambda$.

The RSK correspondence gives a combinatorially described bijection between pairs of standard Young tableaux of the same partition shape $\lambda$ of $n$ (for some $\lambda$) and permutations of $n$. It’s a beautiful bijection, but since the readers of this post will most likely already be familiar with it, I will simply refer the reader to Simon Rubenstein-Salzedo’s clearly-written introduction to RSK.

The upshot is that there is one higher Specht polynomial for each pair of standard Young tableaux $(S,T)$ of the same shape, denoted $F_T^S$. The degree of $F_T^S$ is given by the charge statistic on $S$, defined as follows. Let $w(S)$ be the reading word of $S$, formed by concatenating the rows of $S$ from bottom to top, and assign subscripts $s(i)$ to the letters $i$ of the reading word recursively as follows. Assign the letter $1$ the subscript $s(1)=0$, and for each $i\ge 1$, if $i+1$ is to the right of $i$ then assign it $s(i+1)=s(i)$, and otherwise $s(i+1)=s(i)+1$. The charge of $S$ is the sum of the subscripts $s(i)$.

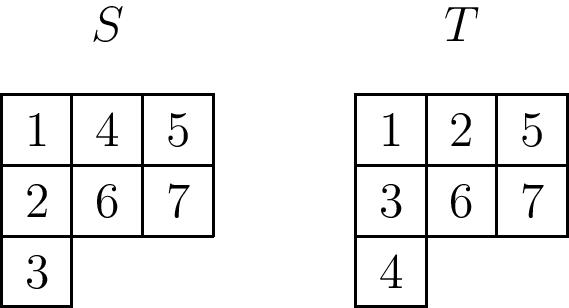
For example, let $S$ and $T$ be the tableaux given below:

Then the charge of $S$ is computed by first forming the reading word \[w(S)=3267145\] and then placing subscripts starting from the letter $1$ according to the rules above: \[3_2 2_1 6_3 7_3 1_0 4_2 5_2\[ Then the charge of $S$ is $2+1+3+3+0+2+2=13$.

The lowest-degree (minimal charge) case occurs when $S=S_0$ is the canonical choice having elements $1,2,3,\ldots,n$ written in order left to right in each row from top to bottom, as in:

In this case we will recover the standard Specht polynomials, and the others are the higher Specht polynomials.

Construction of the Higher Specht polynomials

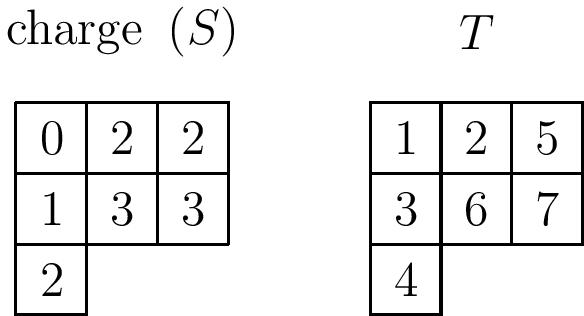
We now have the tools to describe the construction. Given a pair $(S,T)$ of standard Young tableaux of the same shape $\lambda$, let $x_T^{\mathrm{charge}(S)}$ be the monomial $x_1^{i_1}\cdots x_n^{i_n}$ where $i_k$ is the charge subscript on the cell in $S$ corresponding to the cell containing $k$ in $T$. For example, if we fill the boxes of $S$ in the example above with their corresponding subscripts in the charge computation, it looks like:

and we have $x_T^{\mathrm{charge}(S)}=x_2^2x_3x_4^2x_5^2x_6^3x_7^3$.

Then the higher Specht polynomial $F_T^S$ is defined as \[F_T^S(x_1,\ldots,x_n)=\sum_{\tau\in \mathrm{Col}(T)}\sum_{\sigma\in \mathrm{Row}(T)} \mathrm{sgn}(\tau)\tau\sigma x_T^{\mathrm{charge}(S)}\] where $\mathrm{Row}(T)$ and $\mathrm{Col}(T)$ are the subgroups of $S_n$ generated by the permutations of the rows of $T$ and the columns of $T$, respectively.

Notice that this polynomial has degree given by the charge of $S$, which is minimal when $S=S_0$ is the canonical tableau of shape $\lambda$ as described above. And when $S=S_0$, $x_T^{\mathrm{charge}(S)}$ is the product $\prod_{i} x_i^{h_i}$ where $h_i$ is the row of the entry $i$ in $T$. It’s not hard to see that antisymmetrizing this monomial over the column permutations recovers the ordinary Specht polynomial $F_T$. Furthermore, symmetrizing across rows keeps the monomial fixed, and so the higher Specht polynomial $F_T^{S_0}$ is simply a constant multiple of the ordinary Specht polynomial $F_T$.

In general the Specht module $V_\lambda$ occurs once for each tableau $S$ of shape $\lambda$, giving the right multiplicities for each irreducible representation.

Thanks to some Sage code by Nicolas Thiery, we can use this formula to efficiently compute the higher Specht polynomials. Here are the polynomials for $n=3$:

\[ 6 \\ 2(y-x) \\ 2(z-x) \\ z(y-x) \\ y(z-x) \\ (y-x)(z-x)(z-y) \]

Note that the first three and the last are (scalar multiples of) ordinary Specht polynomials, and $z(y-x)$ and $y(z-x)$ are two higher Specht polynomials giving another copy of $V_{(2,1)}$.

Generalizations

In their paper, Ariki, Terasoma, and Yamada actually construct a more general version of the higher Specht polynomials that respects the restricted $S_\mu$-module structure of $R_n$ where $S_{\mu_1}\times \cdots \times S_{\mu_k}\subseteq S_n$ is any Young subgroup. It’s also natural to ask whether there are generalizations of the higher Specht modules to related rings such as the Garsia-Procesi modules or even (we can dream!) the Garsia-Haiman modules.