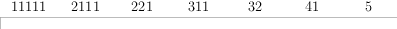Characters of the symmetric group

Last week, I sat down to compute the character table of $S_5$ for the first time in several years.

My first instinct, following what I learned five years ago, was to use the standard tricks for computing character tables: compute the characters of some easily constructed representations, use the fact that the sum of the squares of the dimensions of the irreducible characters is $|S_5|=120$, and use the orthogonality of the rows and columns of the character table to finish it off.

This, however, is rather tedious for a group as large as $S_5$. But I had recently learned that the irreducible representations of the symmetric group are completely classified, and can be constructed using group actions on standard Young tableaux. Was there a way to use this theory to compute each entry of the character table directly?

It turned out that it was possible to laboriously use this theory to compute the characters one at a time, by finding an explicit matrix representation for each irreducible representation. However, I still had a nagging feeling that there should be a faster way to compute the characters.

I dug through the standard references in search of an answer, and I found it: the Murnaghan-Nakayama Rule (thanks to Enumerative Combinatorics, Vol. 2, by Richard Stanley). This concise and elegant method gives a simple combinatorial way of computing the character table of any symmetric group $S_n$. And it goes like this:

Step 1. The conjugacy classes of $S_n$ are the permutations having a fixed number of cycles of each length, corresponding to a partition of $n$ called the shape of the permutation. For instance, the conjugacy classes for $S_5$ have representative elements $\mathbf{1}, (12), (12)(34), (123), (123)(45), (1234), (12345),$ corresponding to the seven partitions $11111, 2111, 221, 311, 32, 41, 5$ of $5$. Since the characters of a group are constant on its conjugacy classes, we index the columns of our character table by these partitions:

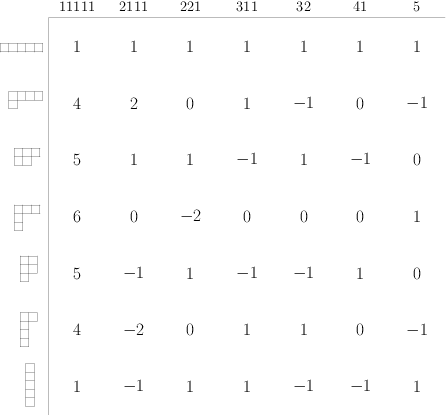
Step 2. There are precisely as many irreducible characters as conjugacy classes, so we can also index the irreducible characters by the partitions of $n$. We represent each partition as a Young diagram and write these down the left of the table:

Step 3: The Murnaghan-Nakayama Rule. We can now calculate the entry in row $\lambda$ and column $\mu$. Let $\mu_1,\mu_2,\ldots$ be the parts of $\mu$ in decreasing order. Drawing $\lambda$ as a Young diagram, define a filling of $\lambda$ with content $\mu$ to be a way of writing a number in each square of $\lambda$ such that the numbers are weakly increasing along each row and column and there are exactly $\mu_i$ squares labeled $i$ for each $i$.

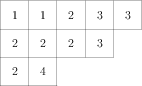
Consider all fillings of $\lambda$ with content $\mu$ such that for each label $i$, the squares labeled $i$ form a connected skew tableaux that does not contain a $2\times 2$ square. (A skew tableau is connected if the graph formed by connecting horizontally or vertically adjacent squares is connected.) Such a tableaux is called a border-strip tableaux, with each label coloring a border strip. For instance, the following is a border-strip tableaux:

For each label in the tableau, define the height of the corresponding border strip to be one less than the number of rows of the border strip. We then weight the tableau by $(-1)^s$ where $s$ is the sum of the heights of the border strips that compose the tableau. (For instance, the heights of the border strips in the above tableaux are $1$, $2$, $1$, and $0$, and so the weight of the tableau is $(-1)^{1+2+1}=1$.) Then, the entry in the character table is simply the sum of these weights.

For example, in the case $n=5$, suppose we are trying to calculate the entry for $\lambda=(3,2)$ and $\mu = 221$. Then the three possible border-strip tableaux are drawn below:

They have weights $1$, $1$, and $-1$, for a total weight of $1+1-1=1$. So, the corresponding entry of the character table is $1$.

That’s all! This gives a quick way to churn out all the entries in the character table:

Using the Murnaghan-Nakayama rule, I was able to compute this table by hand in about 30 minutes. What a gemstone!