Counting ballots with crystals
In my graduate Advanced Combinatorics class last semester, I covered the combinatorics of crystal base theory. One of the concepts that came up in this context was ballot sequences, which are motivated by the following elementary problem about voting:
Suppose two candidates, A and B, are running for local office. There are 100 voters in the town, 50 of whom plan to vote for candidate A and 50 of whom plan to vote for candidate B. The 100 voters line up in a random order at the voting booth and cast their ballots one at a time, and the votes are counted real-time as they come in with the tally displayed for all to see. What is the probability that B is never ahead of A in the tally?
We’ll provide a solution to this classical problem on page 2 of this post. For now, this motivates the notion of a ballot sequence in two letters, which is a sequence of A’s and B’s such that, as the word is read from left to right, the number of A’s that have been read so far is always at least as large as the number of B’s.
For instance, the sequence AABABB is ballot, because as we read from left to right we get the words A, AA, AAB, AABA, AABAB, and AABABB, each of which has at least as many A’s as B’s. On the other hand, the sequence ABBAAB is not, because after reading the first three letters ABB, there are more B’s than A’s.
If we replace the A’s by $1$’s and $B$’s by $2$’s and reverse the words, we obtain the notion of a ballot sequence in $1$’s and $2$’s described in our previous post on crystals. In particular, we say a sequence of $1$’s and $2$’s is ballot if, when we read the word from right to left, there are at least as many $1$’s as $2$’s at each step. So $221211$ and $211111$ are both ballot, but $111112$ and $211221$ are not.
Enumerating all ballot sequences
When I introduced this notion in class, one of my students asked the following.
How many total ballot sequences of $1$’s and $2$’s are there of length $n$?
Now, as in the first question about voting above, the more common version of this type of question is to fix the number of $1$’s and $2$’s in the sequence (the ``content’’ of the word) and ask how many ballot sequences have exactly that many $1$’s and $2$’s. But in this case, the question was asked with no fixed content, resulting in a sum of Littlewood-Richardson coefficients (or, in voting terms, where the voters have not yet decided who they will vote for when they line up, and may vote for either candidate).
To start, let’s try some examples. For $n=0$, there is only one ballot sequence, namely the empty sequence. For $n=1$, there is also just one: $1$. For $n=2$, there are two: $11$ and $21$. For $n=3$, there are three: $111$, $121$, $211$. For $n=4$, there are six: $1111$, $2111$, $1211$, $1121$, $2211$, $2121$. And for $n=5$, there are ten: \[11111, 21111, 12111, 11211, 11121, 22111, 21211, 21121, 12211, 12121\]
The sequence of answers, $1,1,2,3,6,10,\ldots$, so far agrees with the ``middle elements’’ of the rows of Pascal’s triangle:
\[\begin{array}{ccccccccccc}
& & & & & \color{red}1 & & & & & \\
&&&&\color{red} 1&&1 &&&& \\
&&&1&&\color{red} 2&&1&&& \\
&&1&&\color{red} 3&&3&&1&& \\
&1&&4&&\color{red} 6&&4&&1& \\
1&&5&&{\color{red}{10}}&&10&&5&&1
\end{array}\]
More formally, it appears that the number of ballot sequences of $1$’s and $2$’s of length $2n$ is ${2n} \choose {n}$, and the number of length $2n+1$ is ${2n+1}\choose {n}$.
Now, it is possible to prove this formula holds using a somewhat complicated recursive argument, which we will also illustrate on page 2 of this post. But there is also very elegant solution using crystal operators.
Solution using crystals
Let’s recall the definition of the crystal operator $F_1$ on words of $1$’s and $2$’s. Given such a word, we first replace all $2$’s with left parentheses, “$($”, and all $1$’s with right parentheses, “$)$”. We then “cancel” left and right parentheses in matching pairs as shown in the following example.
\[
\begin{array}{ccccccccccc}
2 & 2 & 1 & 1 & 1 & 1 & 2 & 1 & 2 & 2 & 1 \\
( & ( & ) & ) & ) & ) & ( & ) & ( & ( & ) \\
( & & & ) & ) & ) & & & ( & & \\
& & & & ) & ) & & & ( & &
\end{array}
\]
Once all matching pairs have been cancelled, we are left with a subsequence of the form \[)))\cdots))(((\cdots((\] consisting of some number of right parentheses (possibly zero) followed by some number of left parentheses (possibly zero). If there is a $)$ remaining, then $F_1$ changes the rightmost $)$ that was not cancelled to $($, changing that $1$ to $2$ in the original word. The word therefore becomes:
\[
\begin{array}{ccccccccccc}
2 & 2 & 1 & 1 & 1 & 2 & 2 & 1 & 2 & 2 & 1.
\end{array}
\]
Thus $F_1(22111121221)=22111221221$. If there were no $)$ symbols remaining after cancelling, the operator $F_1$ is undefined.
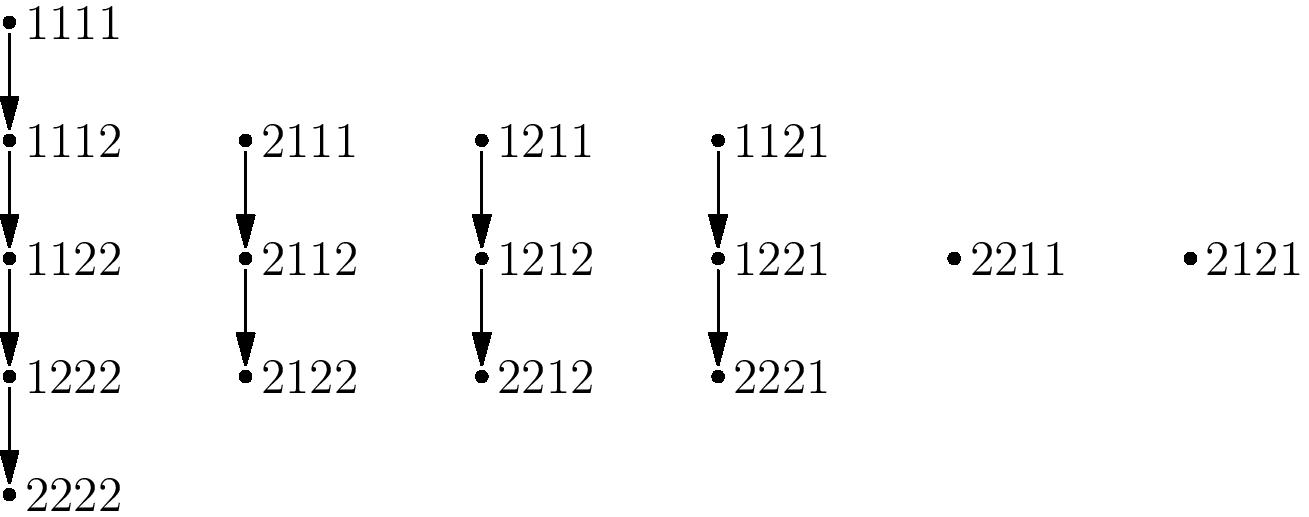
Now, consider the directed graph on all words of $1$’s and $2$’s of length $n$, where we draw an arrow from word $w$ to word $v$ if $F_1(w)=v$. Here is the graph for $n=4$:
This graph will in general be a union of disjoint one-directional chains, since when $F_1$ is defined it is invertible: the unbracketed $1$ that is changed to a $2$ is still unbracketed, and we can identify it as the leftmost unbracketed $2$ in the new word. We write $E_1$ to denote this inverse operator, which changes the leftmost unpaired $2$ to a $1$ if it exists, and is undefined otherwise.
We also cannot have cycles in the $F_1$ graph, because the number of $1$’s always decreases with every application of $F_1$. Thus we have chains of arrows going forward until we reach an element $w$ for which $F_1(w)$ is undefined. Similarly, going backwards along the $F_1$ arrows, we can continue until $E_1$ is undefined, and we call these top elements of each chain the highest weight words.
There are six highest weight words in the above diagram: $1111$, $2111$, $1211$, $1121$, $2211$, $2121$. Notice that these are precisely the two-letter ballot sequences of length $6$!
Indeed, if a word is ballot, then every $2$ as a left parentheses will be cancelled with some $1$ as a right parentheses to its right, so $E_1$ is undefined on such a word. Conversely, if a word is not ballot, consider the first step in the right-to-left reading of the word that has more $2$’s than $1$’s. The $2$ that is encountered at that step cannot be bracketed with a $1$ to its right, because there are not enough $1$’s to bracket with the $2$’s in that suffix. Thus a word is ballot if and only if $E_1$ is undefined, which means that it is at the top of its chain, or highest weight.
Since there is exactly one highest weight word per chain, we have the following.
The number of ballot sequences of length $n$ is equal to the number of chains in the $F_1$ crystal graph on all $2^n$ words of $1$’s and $2$’s of length $n$.
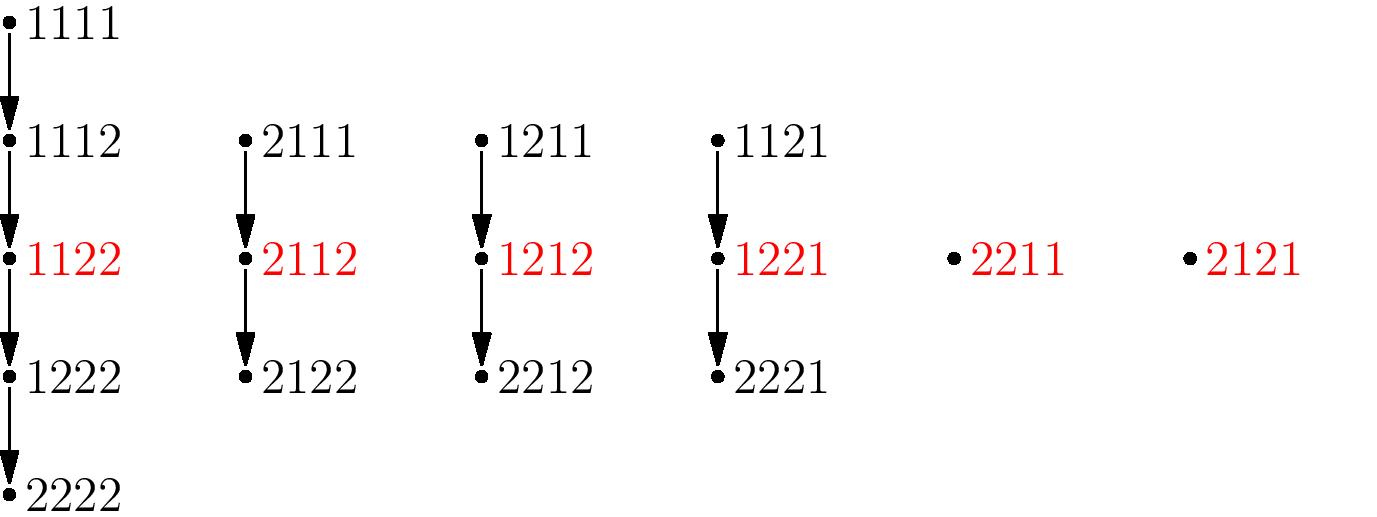
So, to count the ballot words, it suffices to count the chains of the $F_1$ graph. And here’s the key idea: instead of counting the top elements, count the middle ones!
In the picture above, the middle elements of each chain are: \[1122, 2112, 1212, 1221, 2211, 2121\] which is just the set of all words having exactly two $1$’s and two $2$’s, and is clearly counted by ${4}\choose {2}$. Why does this work in general?
Here’s where we need one more fact about the $F_1$ chains: they are “content-symmetric”. If the top element of a chain has $k$ ones and $n-k$ twos, then the bottom element has $n-k$ ones and $k$ twos. This is because the top element, after pairing off an equal number of $2$’s and $1$’s by matching parentheses, has a certain number of unpaired $1$’s, which then all get changed to $2$’s one step at a time as we move towards the bottom of the chain. In particular, the middle element of each chain has exactly as many $1$’s as $2$’s (or, if $n$ is odd, the two “middle elements” have one more $1$ than $2$ and one less $1$ than $2$ respectively.)
Finally, since the graph is drawn on all $2^n$ possible words, every word having the same number of $1$’s as $2$’s (or off by $1$ in the odd case) occurs in exactly one chain. It follows that there is a bijection between the chains and these words, which are enumerated by ${2n}\choose {n}$ for words of length $2n$, and ${2n+1}\choose {n}$ for words of length $2n+1$.
Now let’s consider a more elementary approach.
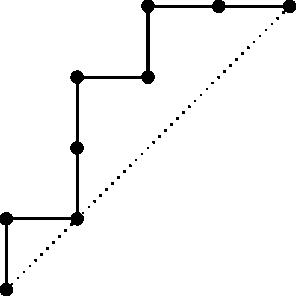
The voting problem stated at the start of this post asks for the probability that a random sequence containing exactly fifty $1$’s and fifty $2$’s is ballot. So, let’s count how many ballot sequences of length $2n$ have the same number of $1$’s and $2$’s. Such words are also called Dyck words, and are in natural bijection with Dyck paths of height $n$, which are the lattice paths from $(0,0)$ to $(n,n)$ that stay weakly above the diagonal line $x=y$ in the plane.
To create a Dyck path from a Dyck word, read the word from right to left, and, starting from $(0,0)$, move up one step for each $1$ that you read, and right one step for each $2$ that you read. For instance, the word $22121121$ corresponds to the Dyck path:
Now, it is well-known that the number of Dyck paths of height $n$ is the $n$-th Catalan number $C_n$, and that an explicit formula for the Catalan numbers is given by $C_n=\frac{1}{n+1}{2n\choose n}$.
For the voting problem with 100 voters, it follows that there are $C_50=\frac{1}{51}{100\choose {50}}$ ballot sequences, out of a sample space of ${100}\choose {50}$ total possible sequences of votes. Therefore, the probability that one candidate is never ahead of the other in the count is \[\frac{1}{51}{100\choose {50}}/\ {100\choose {50}}=\frac{1}{51}.\]
Counting ballot sequences recursively
We now give a more elementary way, without using crystals, to count the total number of two-letter ballot sequences of length $2n$ or $2n+1$ (with any number of $1$’s and $2$’s). Let $B_{m}$ be the number of two-letter ballot sequences of length $m$ for any $m$.
We first show that \[B_{2n}=2B_{2n-1}\] for all $n\ge 1$. Indeed, any ballot sequence of length $2n-1$ has at least one more $1$ than $2$ since there are an odd number of letters total. Thus, we may place either a $1$ or $2$ at the start of the word to result in another ballot sequence of length $2n$. Conversely, given a ballot sequence of length $2n$, its final $2n-1$ letters form a ballot word. This gives a two-to-one correspondence between the ballot words of length $2n$ and those of length $2n-1$, so the claim holds.
Next, we show that \[B_{2n+1}=2B_{2n}-C_n\] for all $n\ge 0$. Indeed, to form a ballot sequence of length $2n+1$, we may either add a $1$ or $2$ to the start of a ballot sequence of length $2n$ that has strictly more $1$’s than $2$’s as above, or we may add a $1$ (but not a $2$!) to a ballot sequence that has exactly the same number of $1$’s as $2$’s. Since the latter type are Dyck words, counted by the $n$-th Catalan number, we have \[B_{2n+1}=2\cdot (B_{2n}-C_n)+1\cdot C_n=2B_{2n}-C_n.\]
Finally, using the explicit formula $C_n=\frac{1}{n+1}{2n\choose n}$, we can check that our guesses $B_{2n}={2n\choose {n}}$ and $B_{2n+1}={2n+1\choose {n}}$ satisfy these recursions. Indeed, we have \[\begin{eqnarray*}
{2n}\choose {n}&=&\frac{(2n)!}{n!n!} \\
&=&\frac{2n}{n}\frac{(2n-1)!}{(n-1)!n!} \\
&=&2{2n-1\choose {n-1}}, \end{eqnarray*}\] so the formulas satisfy the recursion $B_{2n}=2B_{2n-1}$.
We also have \[\begin{eqnarray*}2\binom{2n}{n}-\frac{1}{n+1}{2n\choose {n}}&=&\frac{2(n+1)-1}{n+1}{2n\choose {n}} \\ &=&\frac{(2n+1)(2n)!}{(n+1)n!n!} \\ &=&{2n+1}\choose {n}\end{eqnarray*}\] so the formulas satisfy $B_{2n+1}=2B_{2n}-C_n$. Since we have already checked the initial conditions, the result follows.
Corollary: A proof of the Catalan explicit formula
Notice that our crystal proof did not at all depend on the explicit formula for the Catalan numbers, but our second proof did. We can therefore combine these two methods to give a crystal-theoretic proof of the beautiful formula $C_n=\frac{1}{n+1}{2n\choose {n}}$.