Knuth equivalence on a necklace

Lately, I’ve been working on some open problems related to a Young tableau operation called catabolism, which involves some interesting tableaux combinatorics. While working the other day, I encountered a simple and beautiful fact that I never would have expected.

Suppose we have a word $w$ whose letters are from the alphabet $\{1,\ldots,n\}$ (allowing repeated letters). A Knuth move is one of the following:

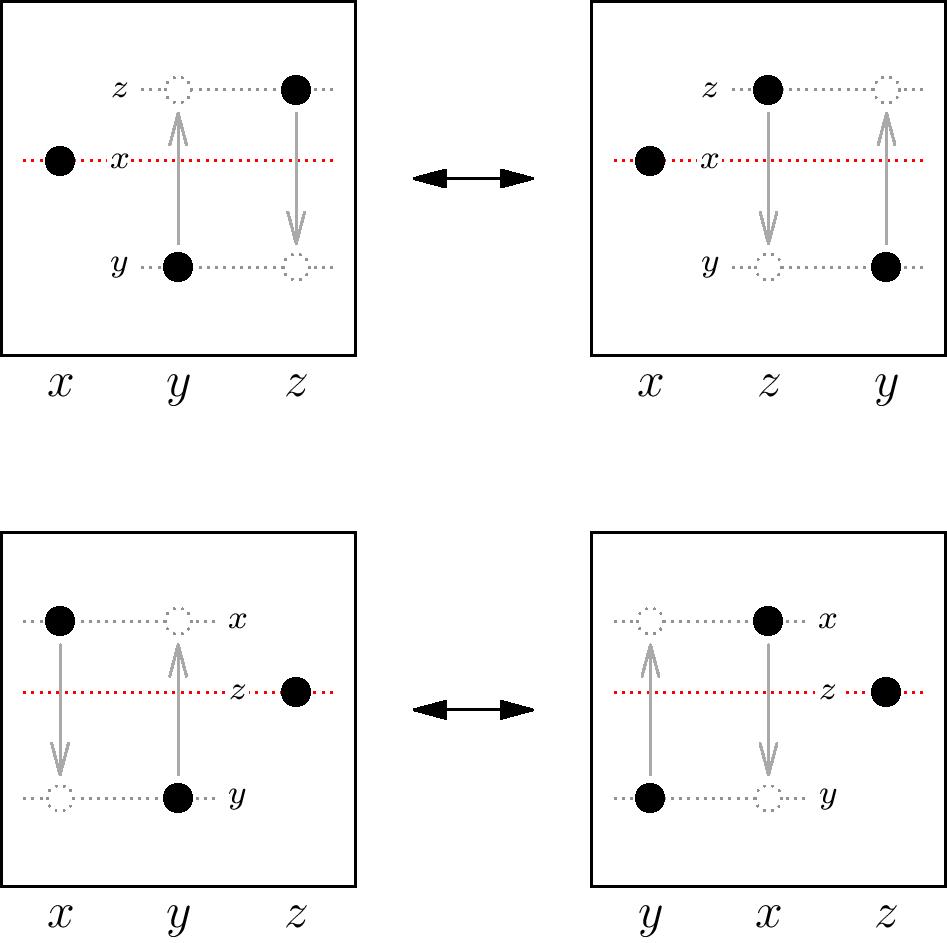
1. Given three consecutive letters $xyz$ with $x>y$ and $x\le z$, replace $xyz$ with $xzy$, or vice versa (replace $xzy$ with $xyz$).

2. Given three consecutive letters $xyz$ with $z\ge y$ and $z\lt x$, replace $xyz$ with $yxz$, or vice versa (replace $yxz$ with $xyz$).

In other words, if you have three consecutive letters and either the first or the third lies between the other two in size, the end letter acts as a pivot about which the other two letters switch places. Visually:

In the case of a tie, think of the repeated letters as getting larger as you go to the right. For instance, in the word $211$, the rightmost $1$ is ``larger’’ than the middle $1$, so $211$ can be replaced with $121$ by switching the left $1$ and the $2$.

If two words can be reached from each other by a sequence of Knuth moves, we say they are Knuth equivalent. For instance, $12143$ is equivalent to $24113$ via the sequence of moves:

12143 21143 21143 21413 21413 24113 In addition, not all words on the same letters are equivalent: the word $123456$, for instance, has no valid Knuth moves and so it is only equivalent to itself.

Since the moves are invertible, Knuth equivalence sorts all words into Knuth equivalence classes. In 1970, Donald Knuth realized that these equivalence classes are in one-to-one correspondence with semistandard Young tableaux, which has made them very useful in algebraic combinatorics.

Recently, I needed to understand what happens when you allow the Knuth moves to ``wrap around at the edge’’. In other words, think of the word as being on a necklace or counterclockwise-oriented circle, and allow the same Knuth moves as before. For instance, $123456$ is now equivalent to $623451$ since the $5$ is between the next two letters, $1$ and $6$.

Now, we get ``cyclic’’ Knuth equivlance classes. How do these relate to the original Knuth equivalence classes? It turns out that there is only one cyclic Knuth equivalence class for any given collection of letters. That is, for any two arrangements of the same collection of letters around a necklace, there is a sequence of cyclic Knuth moves that takes one to the other.

It’s a nice fact - can you see why it’s true?