The 3x+1 problem!

I have exciting news today: The first ever joint paper by Monks, Monks, Monks, and Monks has been accepted for publication in Discrete Mathematics.

These four Monks’s are my two brothers, my father, and myself. We worked together last summer on the notorious $3x+1$ conjecture (also known as the Collatz conjecture), an open problem which is so easy to state that a child can understand the question, and yet it has stumped mathematicians for over 70 years.

The $3x+1$ problem asks the following: Suppose we start with a positive integer, and if it is odd then multiply it by $3$ and add $1$, and if it is even, divide it by $2$. Then repeat this process as long as you can. Do you eventually reach the integer $1$, no matter what you started with?

For instance, starting with $5$, it is odd, so we apply $3x+1$. We get $16$, which is even, so we divide by $2$. We get $8$, and then $4$, and then $2$, and then $1$. So yes, in this case, we eventually end up at $1$.

That’s it! It’s an addictive and fun problem to play around with (see http://xkcd.com/710/), but it is frustratingly difficult to solve completely.

So far, it is known that all numbers less than $20\cdot 2^{58}$, or about $5.8$ billion billion, eventually reach $1$ when this process is applied. (See Silva’s and Roosendaal’s websites, where calculations are continually being run to verify the conjecture for higher and higher integers.)

But what about the general case?

Let’s define the Collatz function $T$ on the positive integers by: $T(x)=\begin{cases}\frac{3x+1}{2} & x\text{ is odd} \\ \frac{x}{2} & x\text{ is even}\end{cases}$.

Then the conjecture states that the sequence $x, T(x), T(T(x)), T(T(T(x))),\ldots$ has $1$ as a term. Notice that $T(1)=2$ and $T(2)=1$, so $1$ is a cyclic point of $T$.

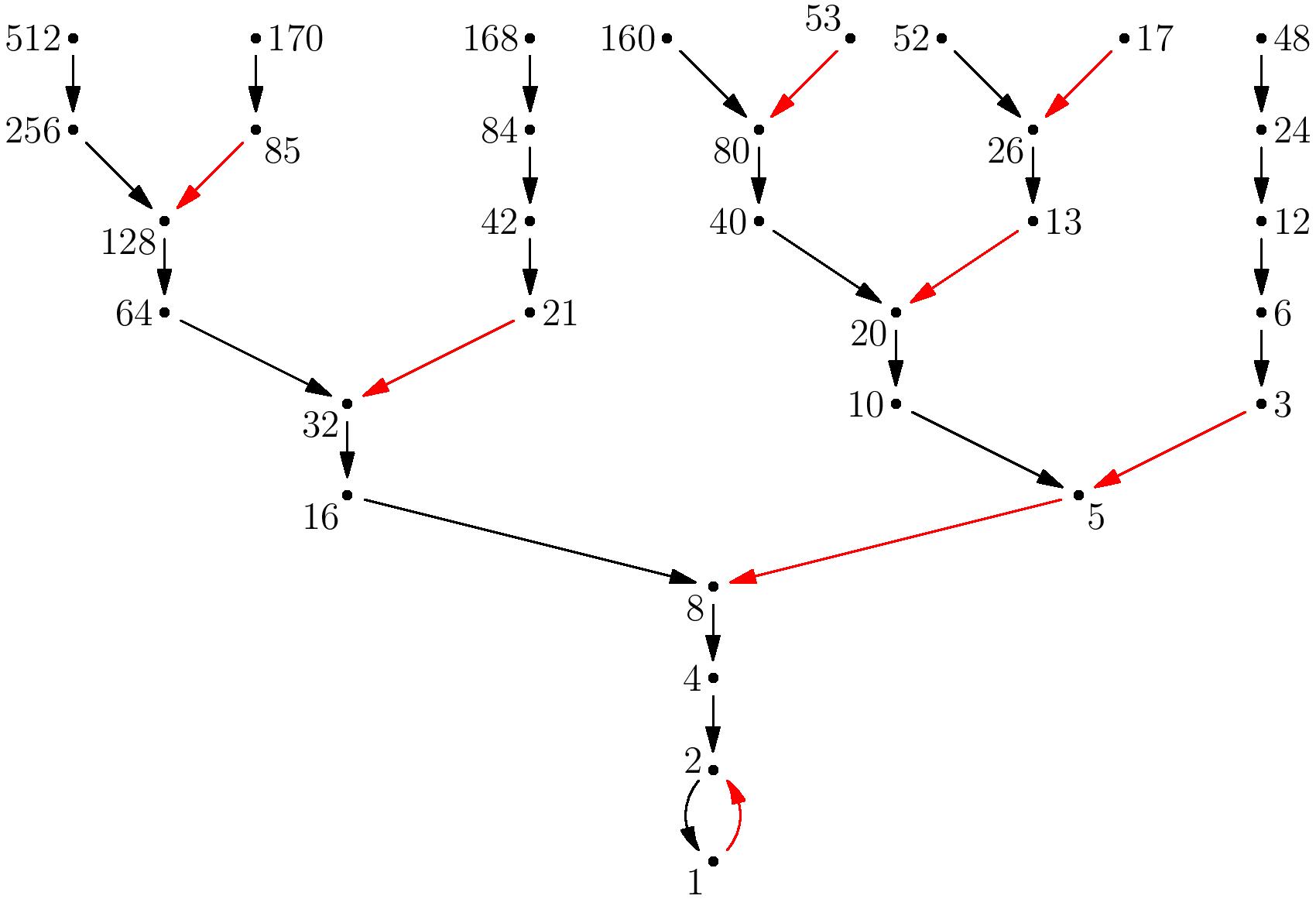
We can draw a graph on the positive integers in which we connect $x$ to $T(x)$ with an arrow for all $x$, and color it red if $x$ is odd and black if $x$ is even. The portion of the graph near $1$ looks like this:

We just want to show that this graph is connected - that there are no other components with very large integers that don’t connect back to $1$.

Last summer, we started out with some previous ideas and partial progress. In 2006, one member of our family research team, my brother Ken M. Monks, demonstrated that it suffices to prove the conjecture for some arithmetic sequence in the Collatz graph. (The paper is available here.) With this as a starting point, we worked to understand how arithmetic sequences are distributed across the Collatz graph. Where do they occur? How far apart are their elements?

By the end of the summer, we realized that there was some beautiful structure in the Collatz graph lying before us. We proved several surprising number-theoretic results, for instance, that every $T$-orbit must contain an integer congruent to $2$ modulo $9$.

We’re not sure if this will lead to a proof of the conjecture, but we found a few big gemstones that might give us a boost in the right direction. A preprint of the paper can be found here:

http://arxiv.org/abs/1204.3904

Enjoy, and feel free to post a comment with any ideas on the conjecture you may have!