Equilateral triangles in the complex plane

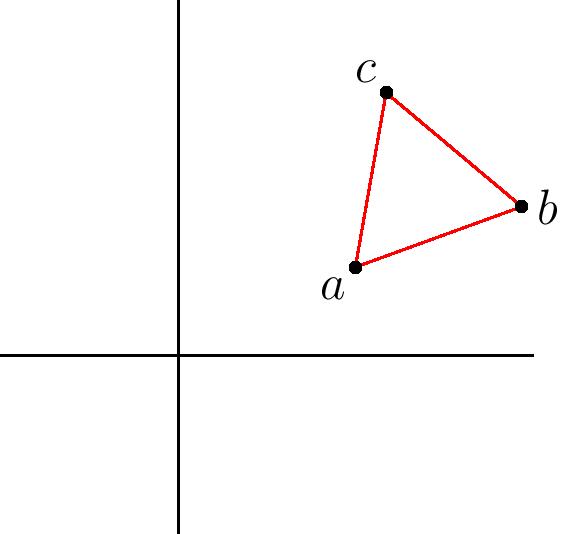
I came across an exercise in Ahlfors’ Complex Analysis the other day that got me thinking. The exercise asked to prove that the complex numbers $a$, $b$, and $c$ form the vertices of an equilateral triangle if and only if $a^2+b^2+c^2=ab+bc+ca.$ It struck me as quite a nice, simple, and symmetric condition.

My first instinct, in going about proving this, was to see if the condition was translation invariant, so that one of the points can be moved to the origin. Indeed, if we subtract a constant $z$ from each of $a,b,c$ the equation becomes $(a-z)^2+(b-z)^2+(c-z)^2=(a-z)(b-z)+(b-z)(c-z)+(c-z)(a-z),$ which simplifies to the original equation after expanding each term. So, we can assume without loss of generality that $a=0$, and we wish to show that $0$, $b$, and $c$ form the vertices of an equilateral triangle if and only if $b^2+c^2=bc$.

To finish up, since we can multiply $b$ and $c$ by a constant scaling factor without changing the condition, we can further assume that $b=1$. So then $1+c^2=c$, implying that $c=\frac{1}{2}\pm \frac{\sqrt{3}}{2}i$. So indeed, the three points form an equilateral triangle. QED.

This proof works, but is somehow deeply unsatisfying. I wanted to find a more ``symmetric’’ proof, that didn’t involve moving one of the points to an origin and another to an axis. Such a coordinate-free condition should have a coordinate-free proof.

Another way to approach it is to first manipulate the condition a bit: \begin{eqnarray*} a^2+b^2+c^2-ab-bc-ca&=& 0 \\ 2a^2+2b^2+2c^2-2ab-2bc-2ca &=& 0 \\ (a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ac+a^2) &=& 0 \\ (a-b)^2+(b-c)^2+(c-a)^2=0 \end{eqnarray*}

So, we have re-written the equation as a sum of three squares that equals $0$. (Too bad we’re looking for complex and not real solutions!)

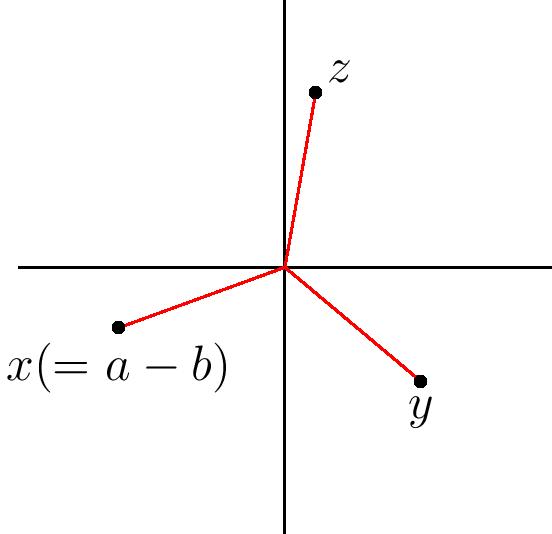
Setting $x=a-b$, $y=b-c$, and $z=c-a$, the condition now becomes $x^2+y^2+z^2=0$, along with the additional equation $x+y+z=0$.

Notice that $x$, $y$, and $z$ are, in some sense, the sides of the triangle $abc$ as vectors. So, we are trying to show that if $x^2+y^2+z^2=0$ and $x+y+z=0$, then $x$, $y$, and $z$ all have the same distance to $0$ and are spaced $120^\circ$ apart from each other around the origin. This is starting to sound more tractable.

In fact, upon closer inspection, we are simply studying the intersection of two curves in the complex projective plane. The points in this plane are equivalence classes of triples $(x:y:z)$, not all zero, up to scaling by a complex number (which is dilation and rotation, geometrically). So, we can think of the equation $x^2+y^2+z^2=0$ as a quadratic curve in this plane, and the equation $x+y+z=0$ as a line, and we simply want to know where these curves intersect.

Intuitively, a quadratic curve (such as a circle or a parabola) and a line should intersect in at most 2 points. Indeed, Bezout’s theorem tells us that two complex projective curves of degrees $d$ and $e$ intersect in at most $de$ points. Here, $d$ and $e$ are $2$ and $1$, so we have at most $2$ solutions $(x:y:z)$ to the equations $x^2+y^2+z^2=0$ and $x+y+z=0$.

But we already know two solutions: first, any $x,y,z$ that are equal in norm and spaced at $120^\circ$ angles around $0$ will satisfy $x+y+z=0$, since they form an equilateral triangle with its centroid at the origin. Since squaring them will double their angles, $x^2$, $y^2$, and $z^2$ are at angles of $240^\circ$ from each other, which is the same as $120^\circ$ in the opposite direction! So, $x^2+y^2+z^2=0$ as well in this case.

Moreover, such $x$, $y$, and $z$ are unique up to dilation, rotation, and reflection of the equilateral triangle (say, interchanging $x$ and $y$). But scaling or rotating $x$, $y$, and $z$ by a complex constant does not change the point $(x:y:z)$, and so the only other distinct point is formed by reflecting the triangle. (Thanks to Bryan Gillespie for this helpful geometric insight!)

So we already know two distinct solutions, and by Bezout’s theorem there cannot be any others. It follows that the original triangle $abc$ must be equilateral.

Somehow more satisfactorily, QED.