Combinatorial species

Just last month, I took my Ph.D. qualifying exam at Berkeley. It was a grueling three-hour oral exam, but from it came a gemstone that simply must be shared!

The very first question I was asked was from my advisor, Mark Haiman: ``Enumerate [count] the labeled plane trees on $n$ vertices.’’

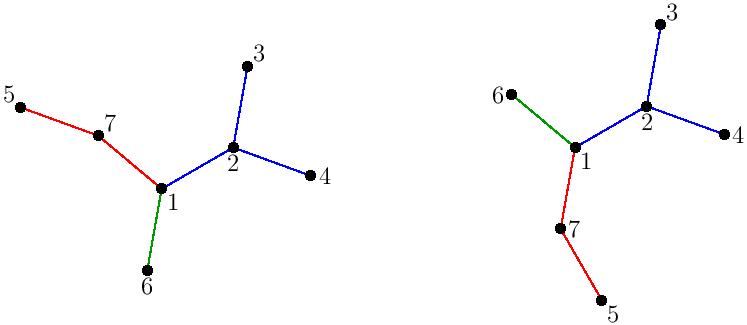
More precisely, let $n$ be a positive integer, and define a labeled plane tree to be a tree with vertices labeled $1,2,\ldots,n$, along with a cyclic ordering of the branches attached to each vertex. (The name ``plane tree’’ refers to the fact that the orderings of the branches determine an embedding of the tree into Euclidean space up to homotopy equivalence.) For instance, say we had the following trees drawn in the plane:

They are isomorphic as graphs but not as plane trees, because the branches around the vertex $1$ have different clockwise cyclic orderings.

So how do we count these trees?

Let’s get our hands dirty and start counting them by brute force. Letting $p_n$ denote the number of distinct plane trees up to isomorphism, it isn’t hard to find that $p_0=0$, $p_1=1$, $p_2=1$, $p_3=3$, $p_4=20$, and with a bit more work, $p_5=210$. Hmm. No obvious pattern jumps out immediately, and the computation gets difficult very quickly as $n$ increases.

Perhaps we can find a generating function for $p_n$ instead. And here is where species play a role.

So what is a species?

Formally, a species is a functor from the category $N$ of finite sets to itself, where the morphisms in $N$ are bijections of sets.

Less formally, a species $S$ is an assignment, for each $n\ge 0$, of the set $[n]=\{1,2,\ldots,n\}$ to a finite set $S([n])$, along with a rule for ``relabeling.’’ The relabeling rule then determines a unique finite set $S(A)$ for any given finite set $A$.

For instance, we can define the ``species of cyclic permutations” $C$ by \[C([n])=\{\text{cyclic permutations of }1,2,\ldots,n\}.\] Then for any $A=\{a_1,\ldots,a_n\}$ and any bijection $\phi:[n]\to A$, we have \[C(A)=\{\text{cyclic permutations of }a_1,a_2,\ldots,a_n\},\] and there is a natural bijection $C([n])\to C(A)$ given by re-labeling the permutations according to $\phi$.

Species serve as an excellent organizational tool for manipulating generating functions. The exponential generating function of a species $S$ is the function \[\widetilde{S}(x)=\sum_{n=0}^\infty \frac{|S([n])|}{n!}x^n.\] Recall that we can add, multiply, and sometimes compose exponential generating functions, and it is useful to define corresponding operations on species:

Addition of species: Given two species $S,T$, we define the species $S+T$ by \[(S+T)([n])=S([n])\sqcup T([n]),\] with the relabeling rule naturally inherited from $S$ and $T$. It is easy to see that this corresponds to addition of exponential generating functions: $\widetilde{S+T}=\widetilde{S}+\widetilde{T}$.

Example: Let $E$ be the species of even permutations and $O$ the species of odd permutations. Let $P$ be the species of all permutations. Then $E+O=P$.

Multiplication of species: Given species $S$ and $T$, we define the species $S\cdot T$ as follows: $(S\cdot T)([n])$ is the set of tuples $(A_1,A_2,\alpha,\beta)$ where $A_1$ and $A_2$ form a partition of $[n]$, and $\alpha\in S(A_1)$ and $\beta\in S(A_2)$. We also have $\widetilde{S\cdot T}=\widetilde{S}\cdot \widetilde{T}$.

Example: Every permutation can be decomposed into a product of even cycles and odd cycles, so if $A$ is the species of permutations having only even cycles and $B$ is the species of permutations having only odd cycles, then $A\cdot B=P$.

Composition of species: Given species $S$ and $T$ with $T(\emptyset)=\emptyset$, we define $(S\odot T)([n])$ to be the set of tuples $(A_1,\ldots,A_k,\alpha_1,\ldots \alpha_k,\beta)$ where $A_1,\ldots,A_k$ form a partition of $[n]$, each $\alpha_i\in T(A_i)$, and $\beta\in S(\{A_1,\ldots, A_k\})$. This corresponds to composition of exponential generating functions: $\widetilde{S\odot T}=\widetilde{S}\circ \widetilde{T}$, which is only well-defined when $\widetilde{T}(0)=0$.

Example: Permutations can be uniquely written as a union of disjoint cycles. Each of the cycles has a $C$-structure and the cycles themselves have the trivial structure, so if $E$ is the ``trivial species’’ sending each $[n]$ to $\{1\}$, then $E\odot C=P$.

Now that we have the machinery of species, the plane trees problem cracks right open. We will use the following species in our computation:

The species $R$ of rooted plane trees, that is, plane trees with one vertex singled out as the root. Notice that there are $n$ times as many rooted plane trees as plane trees on $n$ vertices, so \[\widetilde{R}(x)=\sum_{n\ge 0} \frac{np_n}{n!}x^n=\sum_{n\ge 0} \frac{p_n}{(n-1)!}x^n.\]
The species $T$ of ordered rooted trees, that is, a rooted tree such that the children of each node starting from the root have a specified linear ordering.
The species $X$ defined by $X([n])=\begin{cases}1 & n=1 \\ \emptyset & n\neq 1\end{cases}$. Notice that \[\widetilde{X}(x)=x.\]
The species $C$ of cyclic orderings of $[n]$. Notice that \[\widetilde{C}(x)=\sum_{n\ge 0}\frac{1}{n}x^n=-\ln(1-x).\]
The species $L$ of linear orderings of $[n]$. Notice that \[\widetilde{L}(x)=\frac{1}{1-x}.\]

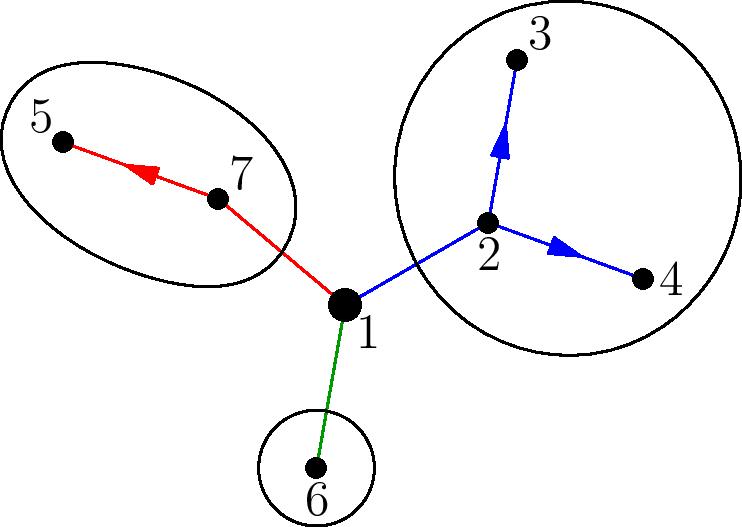
Now, notice that by partitioning a rooted plane tree into its root and its collection of branches with a cyclic ordering on the branches, we have $R=X\cdot (C\odot T)$, as each of the branches can be thought of as a rooted tree along with a linear ordering the children of each node. An example with $1$ as the root, and its branches circled, is shown below.

Taking exponential generating functions, we have \[\begin{equation}\widetilde{R}(x)=x\cdot (-\ln(1-\widetilde{T}(x))),\label{eq:one}\end{equation}\] so we wish to find $\widetilde{T}(x)$. By a similar species argument, $T=X\cdot (L\odot T)$, and so \[\widetilde{T}(x)=\frac{x}{1-\widetilde{T}(x)}.\] Solving, we find \[\widetilde{T}(x)=\frac{1-\sqrt{1-4x}}{2},\] and combining this with equation $\eqref{eq:one}$ we find \[\widetilde{R}(x)=-x\ln\left(\frac{1+\sqrt{1-4x}}{2}\right).\]

We’re almost there: now we just have to extract the coefficients. We have \[\left(\frac{\widetilde{R}(x)}{x}\right)’=\sum_{n\ge 0} \frac{p_{n+2}}{n!} x^n,\] and by our formula for $\widetilde{R}(x)$, \[\begin{eqnarray*} \left(\frac{\widetilde{R}(x)}{x}\right)’ &=& \frac{2}{1+\sqrt{1-4x}}\cdot\frac{1}{\sqrt{1-4x}} \\ &=& \frac{2}{\sqrt{1-4x}}\left(\frac{1-\sqrt{1-4x}}{4x}\right) \\ &=& \frac{1}{2x}(-1+(1-4x)^{-1/2}) \\ &=& \frac{1}{2x}\left(\sum_{k=1}^\infty (-1)^k\binom{-1/2}{k}4^k x^k\right) \\ &=& \sum_{k=0}^\infty (-1)^{k+1} 2^{2k+1} \binom{-1/2}{k} x^k \\ &=& \sum_{k=0}^\infty 2^{2k+1} \frac{(1/2)(3/2)\cdots ((2k+1)/2)}{(k+1)!} x^k \\ &=& \sum_{k=0}^\infty 2^k\frac{(2k+1)!!}{k+1} \frac{x^k}{k!} \\ \end{eqnarray*}\] (Here $(2k+1)!!$ means $1\cdot 3 \cdot 5 \cdot\cdots\cdot (2k+1)$.)

And so, comparing coefficients, we conclude that \[p_{n+2}=2^n\frac{(2n+1)!!}{(n+1)}\] for all $n\ge 0$. Indeed, this checks out with our previous computations of $p_2=1$, $p_3=3$, $p_4=20$, and $p_5=210$.

So species have saved the day… but now that we know the formula for $p_n$, can we find a direct combinatorial proof? I haven’t found one yet, so feel free to comment with ideas!