Positive and recurrent walks

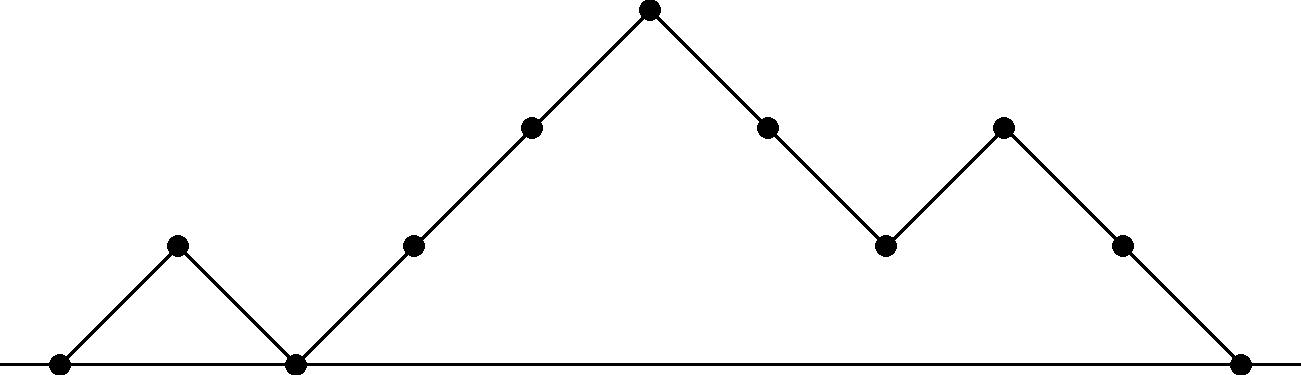
It is rather well-known that the number of up-down walks that start at $0$ and stay nonnegative until ending at $0$ after $2n$ steps is the $n$th Catalan number, $C_n=\frac{1}{n+1}\binom{2n}{n}$. Such paths, in which we either go up by $1$ or down by $1$ at each step and never fall below the $x$-axis, are called Dyck paths. An example for $n=5$ is shown below.

What is not so well-known is that:

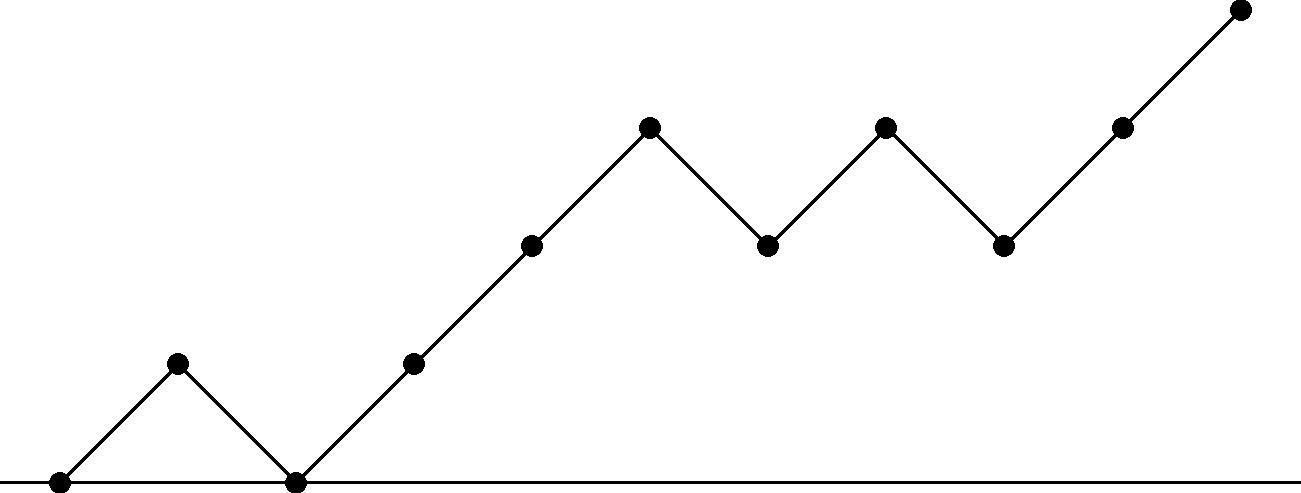
The number of up-down walks of length $2n$ that stay nonnegative, but do not necessarily return to $0$ at the end, is simply $\binom{2n}{n}$.

This fact came up in my research a few days ago, and I figured that this had to be a trivial theorem that was easy to prove. Several hours of failed attempts later, I found myself googling “positive walks central binomial coefficients” and came across a wonderful recent paper of M. van Leeuwen.

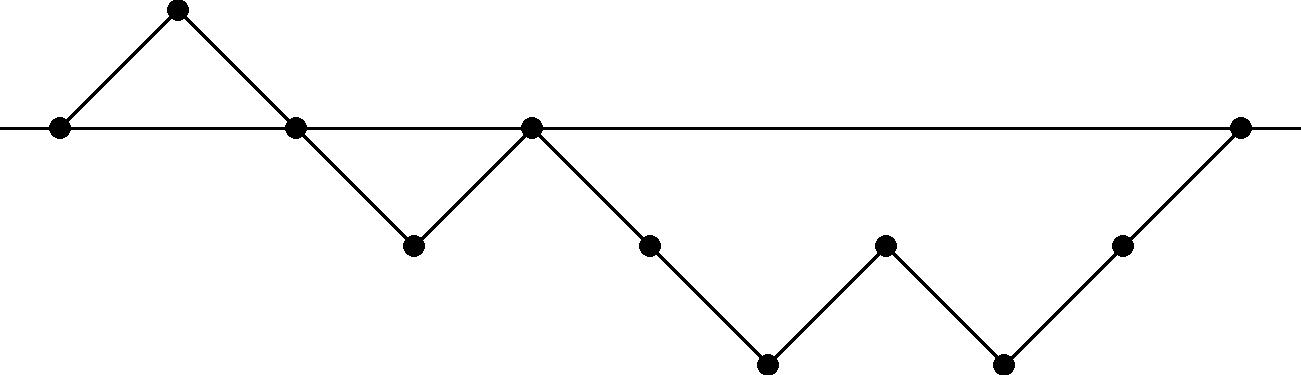
He describes a bijective way of proving this fact by matching the walks with the recurrent (returning-to-zero) walks that are not necessarily positive. Clearly there are $\binom{2n}{n}$ such walks of the latter sort, since they can be thought of as walks from one corner to the opposite corner on a rotated $n\times n$ grid.

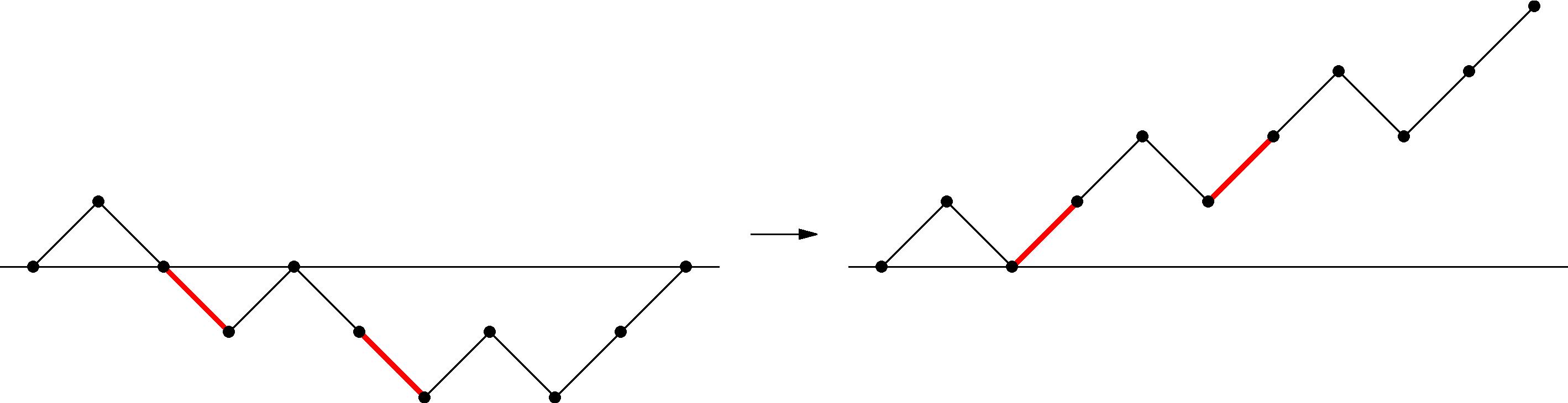
To construct the bijection, consider any recurrent walk from $0$ to $2n$. If the walk is already positive, simply map it to itself. If the walk becomes negative at any point, consider the first times the walk reaches $-1,-2,\ldots,-d$, where $-d$ is the minimum value of the walk. The step just before each of these positions must have been a down-step, and by simply changing each of these $d$ down-steps to an up-step, we end up with a positive walk of length $2n$.

To see that this is bijective, notice that if we had flipped $d$ of the down-steps of the recurrent walk, the last step of the new walk ends at height $2d$. So, to reverse the process, let $2d$ be the ending height of a given positive walk, and we wish to flip $d$ of the up-steps back to down-steps. But the ones we had flipped must be the steps following the last visits to heights $0,1,2,\ldots,d-1$ in the positive walk, by the above construction, so we simply find these visits and flip down the steps following each of them. Beautiful!