Deriving the discriminant of a cubic polynomial through analytic geometric means

This is a contributed gemstone, written by Sushant Vijayan. Enjoy!

Consider a generic cubic equation \[at^3+bt^2+ct+d=0,\] where $a,b,c,d$ are real numbers and $a \neq 0$. Now we can transform this equation into a depressed cubic equation, i.e., one with no $t^2$ term, through means of Tschirnhaus Transformation $t=x-\frac{b}{3a}$, followed by dividing through by $a$. The depressed cubic equation is given by \[x^3+px+q=0\] where $p$ and $q$ are related to $a,b,c,d$ by the relation given here. Setting $p=-m$ and $q=-n$ and rearranging we arrive at \[x^3 =mx+n \hspace{3cm} (1)\] We will investigate the nature of roots for this equation. We begin with plotting out the graph of $y=x^3$:

It is an odd, monotonic, nondecreasing function with an inflection point at $x=0$. The real roots of the equation (1) are the $x$-coordinates of the points of intersection between the straight line $y= mx+n$ and the curve $y=x^3$. It is clear geometrically that however we draw the straight line, as a bare minimum, there would be at least one point of intersection. This corresponds to the fact that all cubic equations with real coefficients have at least one real root.

It is immediately clear that if the slope of the line $m$ is less than $0$, there is only one point of intersection and hence only one real root. On the other hand, the condition $m>0$ is equivalent to demanding that the depressed cubic $y(x)= x^3-mx-n$ has two points of local extrema (which is a necessary, but not sufficient, condition for the existence of three real roots).

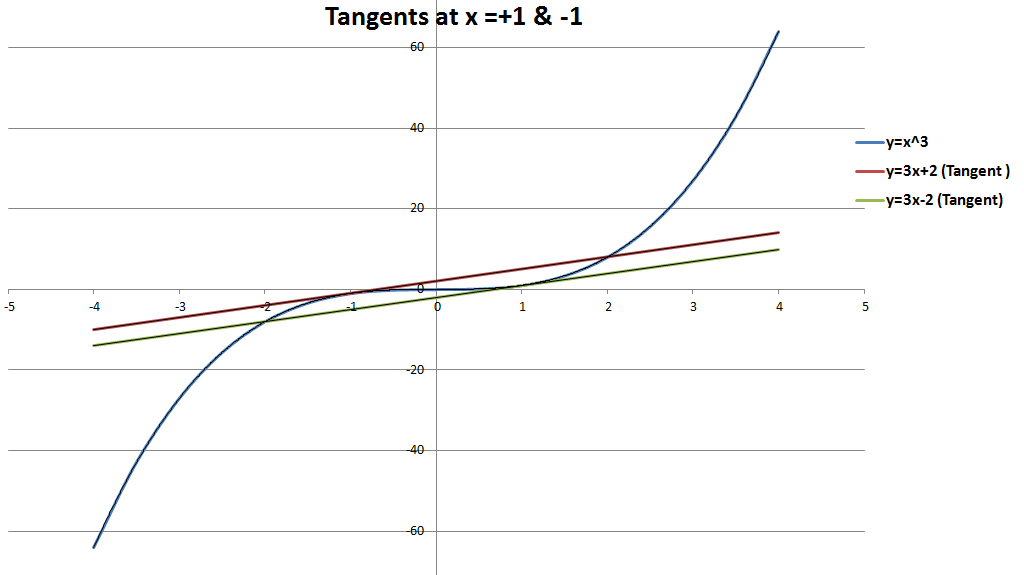
Now the possibility of repeated real roots occur when the straight line is a tangent to the curve $y=x^3$. Hence consider the slope of the function $y=x^3$: \[\frac{dy}{dx}=3x^2\] Now equating the slopes (note $m\ge 0$) we get the tangent points: \[3x^2=m\] \[x=\pm \sqrt{\frac {m}{3} } \]

Equivalently, the tangents are at the two values of $x$ for which \[|x|=\sqrt{\frac {m}{3} }.\]

The corresponding $y$-intercepts for these tangent straight lines are: \[n=\pm \frac{2m}{3}\sqrt{\frac{m}{3}}\] or, in other words, \[|n|=\frac{2m}{3}\sqrt{\frac{m}{3}}\]

Thus for a straight line with a given slope $m\ge 0$ there are only two tangents with  corresponding tangent points and  $y$-intercepts. This would be the case of equation (1) having one real and one real repeated root.

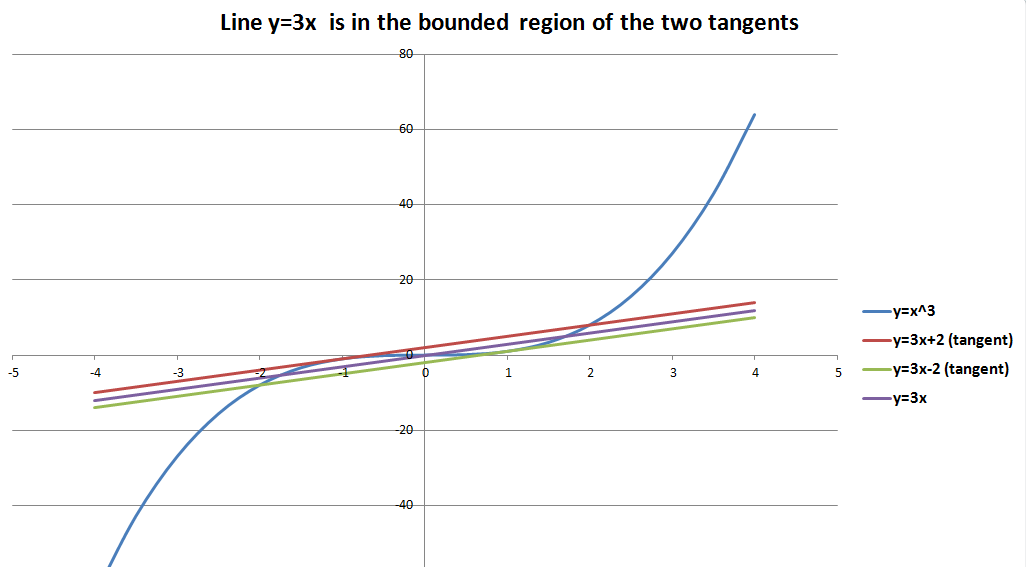
What about the case where the slope is still $m$ but $|n|<\frac{2m}{3}\sqrt{\frac{m}{3}}$?

In this case the straight line is parallel to the two tangent lines (since same slope) and in the region bounded by the two tangent lines. Hence it would necessarily intersect the curve $y=x^3$ at three points. This corresponds to the situation of equation (1) having three real roots.

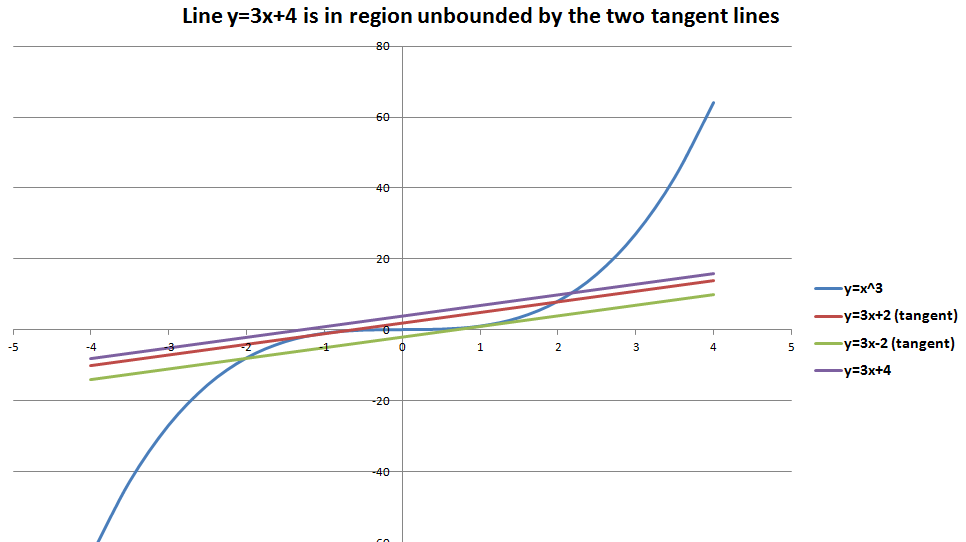
And the case where $ |n| > \frac{2m}{3}\sqrt{\frac{m}{3}}$  corresponds to the area outside the  bounded region of  the two tangent lines and has only one point of intersection.

Hence the necessary and sufficient condition for three real roots (including repeated roots) is given by: \[|n| \le \frac{2m}{3}\sqrt{\frac{m}{3}} \hspace{3cm}(2) \]

We note that the condition $m\ge 0$ is subsumed within the above condition (2), for If $m<0$ then the condition (2) cannot be satisfied.

We note that condition (2) is not a radical expression. We square on both sides and rearrange to arrive at:

\[ \frac{4m^3}{27}-n^2 \ge 0\]

Multiply by 27 and set $\bigtriangleup=4m^3-27n^2 $ to get

\[ \bigtriangleup \ge 0 \]

The $\bigtriangleup $ is the discriminant of the cubic and has all the information required to determine the nature of the roots of the depressed cubic given by equation (1). This may then be written in terms of $a,b,c,d$ by inverting the Tschirnhaus transformation.

A similar exercise may be carried out for the quartic equation, and a similar but albeit more complicated expression can be derived for the discriminant. It would be very interesting to do the same exercise for the quintic and see where it fails (fail it must, otherwise it would contradict Abel’s famous result of insolvability of quintic equations using radical expressions).