A q-analog of the decomposition of the regular representation of the symmetric group

It is a well-known fact of representation theory that, if the irreducible representations of a finite group $\DeclareMathOperator{\maj}{maj} \DeclareMathOperator{\sh}{sh} G$ are $V_1,\ldots,V_m$, and $R$ is the regular representation formed by $G$ acting on itself by left multiplication, then \[R=\bigoplus_{i=1}^{m} (\dim V_i) \cdot V_i\] is its decomposition into irreducibles.

I’ve recently discovered a $q$-analog of this fact for $G=S_n$ that is a simple consequence of some known results in symmetric function theory.

In Enumerative Combinatorics, Stanley defines a generalization of the major index on permutations to standard tableaux. For a permutation \[w=w_1,\ldots,w_n\] of $1,\ldots,n$, a descent is a position $i$ such that $w_i>w_{i+1}$. For instance, $52413$ has two descents, in positions $1$ and $3$. The major index of $w$, denoted $\maj(w)$, is the sum of the positions of the descents, in this case \[\maj(52413)=1+3=4.\]

To generalize this to standard Young tableaux, notice that $i$ is a descent of $w$ if and only if the location of $i$ occurs after $i+1$ in the inverse permutation $w^{-1}$. With this as an alternative notion of descent, we define a descent of a tableau $T$ to be a number $i$ for which $i+1$ occurs in a lower row than $i$. In fact, this is precisely a descent of the inverse of the reading word of $T$, the word formed by reading the rows of $T$ from left to right, starting from the bottom row.

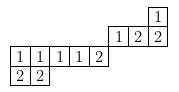
As an example, the tableau $T$ below has two descents, $2$ and $4$, since $3$ and $5$ occur in lower rows than $2$ and $4$ respectively:

So $\maj(T)=2+4=6$. Note that its reading word $5367124$, and the inverse permutation is $5627134$, which correspondingly has descents in positions $2$ and $4$.

(This is a slightly different approach to the major index than taken by Stanley, who used a reading word that read the columns from bottom to top, starting at the leftmost column. The descents remain the same in either case, since both reading words Schensted insert to give the same standard Young tableau.)

Now, the major index for tableaux gives a remarkable specialization of the Schur functions $s_\lambda$. As shown in Stanley’s book, we have \[s_\lambda(1,q,q^2,q^3,\ldots)=\frac{\sum_{T} q^{\maj(T)}}{(1-q)(1-q^2)\cdots(1-q^n)}\] where the sum is over all standard Young tableaux $T$ of shape $\lambda$. When I came across this fact, I was reminded of a similar specialization of the power sum symmetric functions. It is easy to see that \[p_\lambda(1,q,q^2,q^3,\ldots)=\prod_{i}\frac{1}{1-q^{\lambda_i}},\] an identity that comes up in defining a $q$-analog of the Hall inner product in the theory of Hall-Littlewood symmetric functions. In any case, the power sum symmetric functions are related to the Schur functions via the irreducible characters $\chi_\mu$ of the symmetric group $S_n$, and so we get

\begin{eqnarray*} p_\lambda(1,q,q^2,\ldots) &=& \sum_{|\mu|=n} \chi_{\mu}(\lambda) s_{\mu}(1,q,q^2,\ldots) \\ \prod_{i} \frac{1}{1-q^{\lambda_i}} &=& \sum_{\mu} \chi_{\mu}(\lambda) \frac{\sum_{T\text{ shape }\mu} q^{\maj(T)}}{(1-q)(1-q^2)\cdots(1-q^n)} \\ \end{eqnarray*}

This can be simplified to the equation: \begin{equation} \sum_{|T|=n} \chi_{\sh(T)}(\lambda)q^{\maj(T)} = \frac{(1-q)(1-q^2)\cdots (1-q^n)}{(1-q^{\lambda_1})(1-q^{\lambda_2})\cdots(1-q^{\lambda_k})} \end{equation} where $\sh(T)$ denotes the shape of the tableau $T$.

Notice that when we take $q\to 1$ above, the right hand side is $0$ unless $\lambda=(1^n)$ is the partition of $n$ into all $1$’s. If $\lambda$ is not this partition, setting $q=1$ yields \[\sum \chi_\mu(\lambda)\cdot f^{\mu}=0\] where $f^\mu$ is the number of standard Young tableaux of shape $\mu$. Otherwise if $\lambda=(1^n)$, we obtain \[\sum \chi_\mu(\lambda)\cdot f^{\mu}=n!.\] Recall also that $f^\mu$ (see e.g. Stanley or Sagan) is equal to the dimension of the irreducible representation $V_\mu$ of $S_n$. Thus, these two equations together are equivalent to the fact that, if $R$ is the regular representation, \[\chi_R=\sum_\mu (\dim V_\mu) \cdot \chi_{\mu}\] which is in turn equivalent to the decomposition of $R$ into irreducibles.

Therefore, Equation (1) is a $q$-analog of the decomposition of the regular representation. I’m not sure this is known, and I find it’s a rather pretty consequence of the Schur function specialization at powers of $q$.

EDIT: It is known, as Steven Sam pointed out in the comments below, and it gives a formula for a graded character of a graded version of the regular representation.