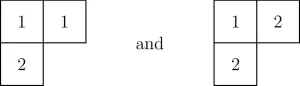The hidden basis
In the last few posts (see here and here), I’ve been talking about various bases for the symmetric functions: the monomial symmetric functions $m_\lambda$, the elementary symmetric functions $e_\lambda$, the power sum symmetric functions $p_\lambda$, and the homogeneous symmetric functions $h_\lambda$. As some of you aptly pointed out in the comments, there is one more important basis to discuss: the Schur functions!
When I first came across the Schur functions, I had no idea why they were what they were, why every symmetric function can be expressed in terms of them, or why they were useful or interesting. I first saw them defined using a simple, but rather arbitrary-sounding, combinatorial approach:
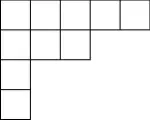
First, define a semistandard Young tableau (SSYT) to be a way of filling in the squares of a partition diagram (Young diagram) with numbers such that they are nondecreasing across rows and strictly increasing down columns. For instance, the Young diagram of $(5,3,1,1)$ is:
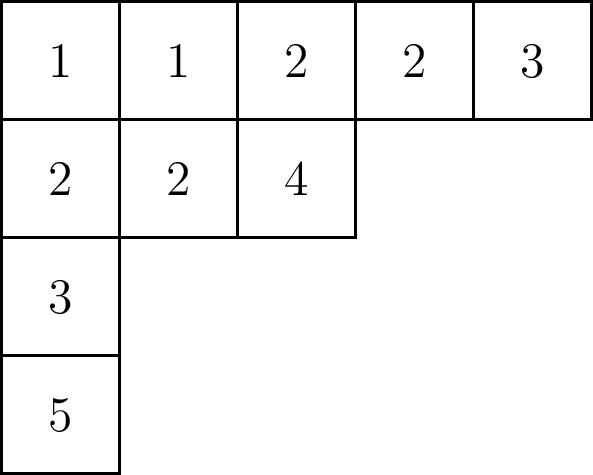
and one possible SSYT of this shape is:
(Fun fact: The plural of tableau is tableaux, pronounced exactly the same as the singular, but with an x.)
Now, given a SSYT $T$ with numbers of size at most $n$, let $\alpha_i$ be the number of $i$`s written in the tableau. Given variables $x_1,\ldots,x_n$, we can define the monomial $x^T=x_1^{\alpha_1}\cdots x_n^{\alpha_n}$. Then the Schur function $s_\lambda$ is defined to be the sum of all monomials $x^T$ where $T$ is a SSYT of shape $\lambda$.
For instance, if $\lambda=(2,1)$, then the possible SSYT’s of shape $\lambda$ with numbers of size at most $2$ are:
So the Schur function $s_{(2,1)}$ in $2$ variables $x$ and $y$ is $x^2y+y^2x$.
This combinatorial definition seemed rather out-of-the-blue when I first saw it. Even more astonishing is that the Schur functions have an abundance of nice properties. To name a few:
- The Schur functions are symmetric. Interchanging any two of the variables results in the same polynomial.
- The Schur functions form a basis for the symmetric functions, Like the elementary symmetric functions, every symmetric polynomial can be expressed uniquely as a linear combination of $s_\lambda$`s.
- The Schur functions arise as the characters of the irreducible polynomial representations of the general linear group. This was proven by Isaac Schur and was the first context in which the Schur functions were defined. Here, a polynomial representation is a matrix representation in which the entries are given by polynomials in the entries of the elements of $GL_n$.
- The transition matrix between the power sum symmetric functions and the Schur functions is precisely the character table of the symmetric group $S_n$. This fact is essential in proving the Murnaghan-Nakayama rule that I mentioned in a previous post.
All of this is quite remarkable - but why is it true? It is not even clear that they are symmetric, let alone a basis for the symmetric functions.
After studying the Schur functions for a few weeks, I realized that while this combinatorial definition is very useful for quickly writing down a given $s_\lambda$, there is an equivalent algebraic definition that is perhaps more natural in terms of understanding its role in symmetric function theory.
The Schur functions can also be defined algebraically in terms of the antisymmetric functions. A polynomial function $f(x_1,\ldots,x_n)$ is antisymmetric if interchanging two of the variables results in the negative of the function. In general, then, a permutation of the variables will change the function by the sign of the permutation.
For instance, $3x^2y-3y^2x$ is antisymmetric, since interchanging $x$ and $y$ negates the function.
In three variables, the function \[x^4y^2z-x^4z^2y-y^4x^2z+y^4z^2x+z^4x^2y-z^4y^2x\] is also antisymmetric. This is an example of a monomial antisymmetric function, constructed by starting with a monomial, in this case $x^4y^2z$, and adding to it every monomial formed by permuting its variables and multiplying by the sign of the permutation. We let $a_\nu$ denote the monomial antisymmetric function with the partition $\nu$ as its sequence of exponents; the function above is $a_{(4,2,1)}$.
Now, suppose we started with the monomial $x^2y^2z$. Because of the repeating exponent $2$, this term cancels with the term $-y^2x^2z$, and so on, leaving $a_{(2,2,1)}=0$. In general, in order for $a_{\nu}$ to be nonzero, it cannot have any repeating exponents, including exponents of $0$.
Thus, the nonzero monomial antisymmetric functions $a_\nu$ are precisely those for which $\nu=\lambda+\delta$ where $\lambda$ is any partition and $\delta=(n-1,n-2,\ldots,1,0)$. (For instance, $(4,2,1)=(2,1,1)+(2,1,0)$.) And, just as with the monomial symmetric functions, it is easy to see that every antisymmetric function can be written as a linear combination of $a_{\lambda+\delta}$`s.
Let’s consider the simplest of these, $a_{\delta}$, and say we are working with three variables $x,y,z$. Then \[a_\delta=x^2y-x^2z-y^2x+y^2z+z^2x-z^2y=(x-y)(x-z)(y-z).\] Notice the nice factorization! In general, $a_\delta$ in $n$ variables $x_1,\ldots,x_n$ factors as $\prod_{i<j}(x_i-x_j)$. (It is a fun challenge to prove this - it is related to the Vandermonde determinant.)
Because of this factorization, $a_\delta$ divides every antisymmetric polynomial: Given any antisymmetric function $f$, it must be divisible by $x_i-x_j$, because setting $x_i=x_j$ makes the polynomial identically zero. So by symmetry, $f$ must be divisible by all of $a_\delta$!
Finally, notice that if we multiply an antisymmetric function $a$ by a symmetric function $s$, the resulting function $sa$ is also antisymmetric. Similarly, the quotient of two antisymmetric functions, if it is a polynomial, is symmetric. We can therefore take the natural monomial basis of the antisymmetric functions, $\{a_{\lambda+\delta}\}$, and turn it into a basis of the symmetric functions simply by dividing by $a_{\delta}$.
So, we define: \[s_\lambda=\frac{a_{\lambda+\delta}}{a_{\delta}}\] And indeed, these are the same Schur functions we saw above! They are algebraically natural, fairly easy to describe combinatorially, and are essential to representation theory. They are not an obvious basis of the symmetric functions, but they are a useful basis nontheless.