Pythagorean triples on a sphere?

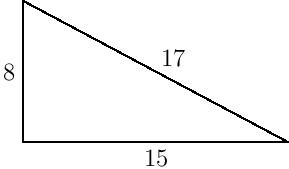
It’s 8/15/17, which means it’s time to celebrate! The three numbers making up the date today form a Pythagorean triple, a triple of positive integers $(a,b,c)$ with $a^2+b^2=c^2$. Indeed, $8^2+15^2=64+225=289=17^2$.

Alternatively, by the Pythagorean theorem, a Pythagorean triple is any triple of positive integers which make up the sides of a right triangle:

It’s exciting when all three sides are integers, since many common right triangles’ lengths involve square roots: $(1,1,\sqrt{2})$, $(1,2,\sqrt{5})$, and $(1,\sqrt{3},2)$, to name a few. And these sides aren’t even rational, which the poor Pythagorean scholar Hippasus discovered by proving that $\sqrt{2}$ is irrational and was subsequently drowned to death by his colleagues, according to some historical accounts. So the ancient Pythagoreans in fact only believed in right triangles having rational side lengths.

Of course, given one Pythagorean triple, like $(3,4,5)$, we can construct infinitely many by scaling the sides: $(6,8,10)$, $(9,12,15)$, etc. (In fact, 12/9/15 was the previous Pythagorean triple day, and 12/16/20 will be the next.) So to classify all Pythagorean triples, it suffices to find the reduced triples, those with no common factors greater than $1$.

So the last reduced Pythagorean triple day was back in 2013 on 12/5/13, and the next one won’t be until 7/24/25!

Constructing Pythagorean triples

It’s well known that there are infinitely many reduced Pythagorean triples as well. One beautiful, famous proof of this derives a parameterization of all triples via geometric means:

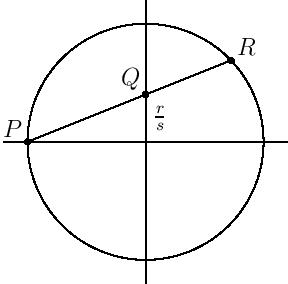
Consider the unit circle and the point $P=(-1,0)$ on the circle. Let $Q=(0,r/s)$ be a rational point on the $y$-axis inside the circle. Then line $PQ$ intersects the circle at a second point $R$, and it turns out $R$ has rational coordinates as well. Some simple algebra with similar triangles (try it, if you haven’t seen it before!) gives us \[R=\left(\frac{r^2-s^2}{r^2+s^2},\frac{2rs}{r^2+s^2}\right).\] But since $R$ lies on the unit circle, if $(x,y)$ are the coordinates of $R$ then $x^2+y^2=1$, and substituting and clearing denominators we have \[(r^2-s^2)^2+(2rs)^2=(r^2+s^2)^2\] (which can also be checked with direct algebraic computation). It follows that $(r^2-s^2,2rs,r^2+s^2)$ is a Pythagorean triple for any integers $r$ and $s$, giving us infinitely many Pythagorean triples. And in fact, for $r$ and $s$ relatively prime of different parity, these triples are reduced.

Spherical considerations

Given that this is a global day to celebrate (assuming you use the standard world calendar), and the Earth is a sphere, I have to wonder whether Pythagorean triples actually exist if drawn on a perfect-sphere approximation of the Earth. First, we’d have to define what we even mean by that - are we measuring in meters? In feet? And what is a right triangle on the surface of a sphere anyway?

The most common definition of a triangle on a sphere is one formed by great circles. A great circle is any circle of maximal diameter around a sphere, in other words, whose plane contains the center of the sphere. So, the equator, the prime meridian, and all longitude lines are great circles on the Earth, but latitude lines are not. A line segment on a sphere is a segment of a great circle, and a (spherical) triangle is a shape formed by three points connected by three (spherical) line segments. The angle between two great circles that intersect is the angle between their planes. (Thanks to Wikipedia for the excellent image below.)

Since our world now has size rather than being a flat plane, let’s set the radius of the Earth to be $1$ unit for simplicity. So we’re working with triangles $ABC$ with a right angle at $C$, and asking when they have rational lengths:

Are there any Pythagorean triples on the unit sphere? Are there infinitely many?

These questions suddenly aren’t very easy. If we scale our sphere down by $\pi/2$ we can get at least one, by taking the equator, the prime meridian, and the $90^\circ$ longitudinal line. This forms a right triangle with all three lengths equal (and all angles right!) and so we can simply scale the Earth to make it any rational lengths we want. But this still doesn’t answer anything about the unit sphere.

There is some hope, however. In this paper by Hartshorne and Van Luijk, the authors show that there are infinitely many Pythagorean triples in the hyperbolic plane, using the Poincare Disk model and some nice hyperbolic trig formulas combined with some Eulerian number theory tricks. So Pythagorean triples are not the sole property of flat Euclidean space.

In addition, there is a ``spherical Pythagorean theorem’’, which in our notation, since the radius of our sphere is $1$, says that \[\cos(c)=\cos(a)\cos(b)\] where $a,b,c$ are the side lengths of the triangle and $c$ is opposite the right angle. And yet, this offers little insight into whether this equation has rational solutions. Trig functions are generally much harder to deal with than polynomials, especially when it comes to solving equations over the rationals.

So, if you have any insights on this problem (or references to papers that have worked on it - I couldn’t find any in an initial search, but I am not very familiar with it), please let me know in the comments! And until then, happy reduced-Pythagorean-triple-in-flat-Euclidean-space day!