Geometry of the real projective plane
I’ll be flying to Nebraska tomorrow to teach at the Math Olympiad Summer Program. One of my more advanced classes will be on projective geometry and how it can help us understand Euclidean geometry. I thought I would share the introduction from my handout, since it is an attempt to demonstrate one of the many reasons projective geometry is such a gemstone:
General projective planes
Let’s start with some general theory. A projective plane is any set $P$, which we call the set of points, and a nonempty collection $L$ of subsets of $P$ called lines, such that the following four axioms hold:
P1: Every pair of distinct points are contained in exactly one line.
P2: Every pair of distinct lines intersect in exactly one point.
P3: There are four distinct points $a,b,c,d\in P$ no three of which lie on a line.
P4: Every line contains at least three points.
Axiom P2 raises some alarms. In Euclidean geometry, we assume that there are parallel lines that never meet, but here, we’re requiring that every pair of lines intersect. So the usual Euclidean plane is not a projective plane.
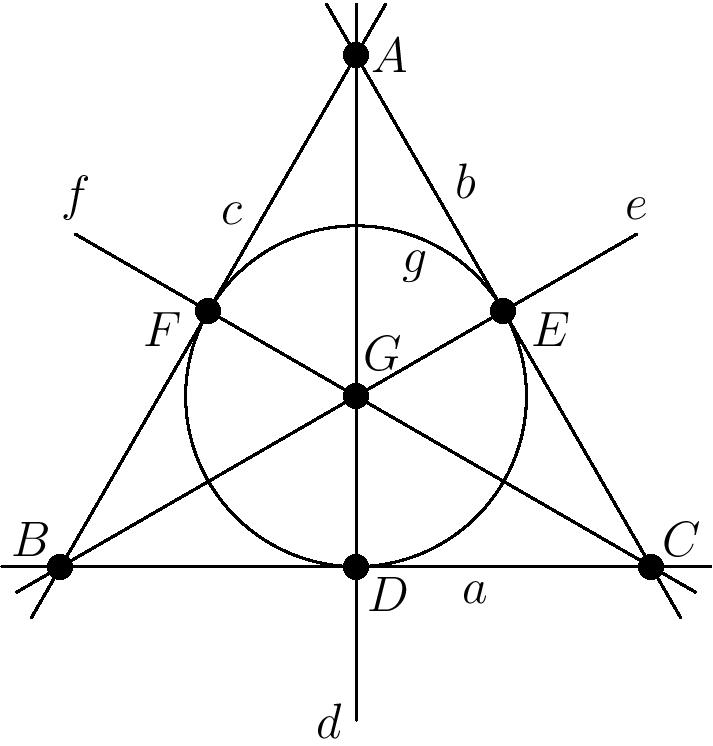
However, there are many interesting projective planes that do come in handy. The simplest and smallest example of a projective plane is known as the Fano plane, or $F_7$, consisting of seven points and seven lines as shown below.
Notice the terms ``point’’ and ``line’’ are interchangeable in the axioms above. We can in fact interchange the roles of points and lines in any projective plane to obtain another projective plane, called the ``dual’’ projective plane. Some projective planes, like the Fano plane above, are even self-dual! (In the diagram above, we can associate each point $A, B, C,\ldots$ with its corresponding lowercase-letter line $a, b, c,\ldots$, and incidence is preserved: points $A$ lies on lines $b$, $c$, and $d$, whereas line $a$ contains points $B$, $C$, and $D$. And so on.)
The projective plane we’ll be dealing with today is the real projective plane, which is an extension of the Euclidean plane that gets rid of those nasty parallel lines by adding an extra line out at infinity. Let’s take a look.
The real projective plane
The real projective plane was first defined by Desargues as an extension of the Euclidean plane $\mathbb{R}^2$ that forces parallel lines to intersect ``at infinity’’, hence creating a plane that satisfies axiom P2 rather than the parallel postulate. When you think about it, this is a rather natural model of things we see in reality. Suppose you are standing on parallel train tracks and looking out towards the horizon along the direction of the tracks. The tracks are parallel, but they appear to converge to a point on the horizon. In this sense, Euclidean geometry is simply a local version of projective geometry; parallel lines are only truly ``parallel’’ near your feet!
To make this rigorous, define a pencil of parallel lines in $\mathbb{R}^2$ to be the set of all lines parallel to a given line in the plane. Then the real projective plane is the set $\mathbb{R}^2\cup l^\infty$ where $l^\infty$ is a set consisting of one point for each pencil of parallel lines in $\mathbb{R}^2$. A line in this plane is then one of:
-
$l^\infty$,
-
Any subset of $\mathbb{R}^2\cup l^\infty$ consisting of a line in $\mathbb{R}^2$ along with the associated point in $l^\infty$.
It’s not hard to see that this satisfies axioms P1-P4 above. Any two lines that were parallel in $\mathbb{R}^2$ now meet at the point at infinity corresponding to their pencil.
Homogeneous coordinates
There is another, more symmetric way to define the real projective plane. We can think of a point in the real projective plane as a ratio $(a:b:c)$ of three real numbers, not all zero, called its homogeneous coordinates. (Since we only care about the ratio between the numbers, $(2:4:5)$ and $(6:12:15)$ describe the same point.)
A line is then defined as the set of solutions $(a:b:c)$ to a linear equation \[\alpha x +\beta y + \gamma z=0\] for some fixed $\alpha$, $\beta$, $\gamma$.
It’s not hard to see why this is equivalent to our first definition of the real projective plane. Each point either has $z=0$ or $z\neq 0$. Those with $z\neq 0$, we can normalize so that $z=1$, and then take $(x:y:1)$ to be the point $(x,y)$ in $\mathbb{R}^2$. The points with $z=0$ then form the new line $l^\infty$, where $(x:y:0)$ corresponds to the direction with ``slope’’ $y/x$ (or the vertical direction, if $x$ is $0$.)
Exercise. Show that the unit circle, expressed in homogeneous coordinates, is described by the equation \[x^2+y^2=z^2.\] Why doesn’t the equation $x^2+y^2=1$ make sense in the projective plane?
Reciprocation (pole and polar)
Like the Fano plane, the real projective plane is self-dual. How can we exchange the points and lines in such a way that collinearity becomes concurrency and vice versa? The answer lies in the pole of a line and the polar of a point.
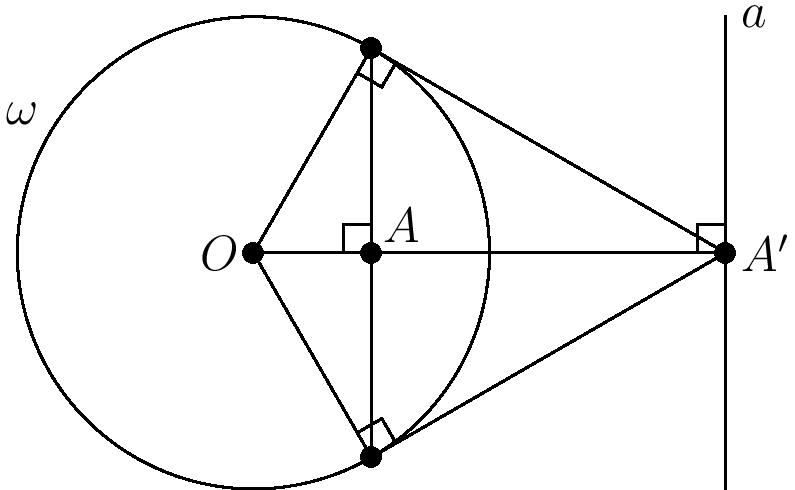
Polar: Fix a circle $\omega$ in the Euclidean plane with center $O$. Let $A$ be any point in the projective plane, and let $A’$ be its inverse about $\omega$ (where all the points at infinity invert to $O$), and let $a$ be the line through $A’$ that is perpendicular to line $OA’$ (or $OA$, if $A’=O$). Then $a$ is the polar of $A$.
Pole: of a line $a$ is the reverse construction. First, the pole of the line at infinity is $O$. Now, given a line $a$ other than the line at infinity, let $A’$ be the foot of the altitude from $O$ to $a$ and let $A$ be the inverse of $A’$ about $\omega$. Then $A$ is the pole of $a$ (and $a$ is the polar of $A$.)
Exercise. Show that $A$ lies on the polar of $B$ if and only if the polar of $A$ passes through $B$.
We now know that reciprocation, the transformation about a circle that replaces each point with its polar and each line with its pole, interchanges lines and points in a way that preserves indicence. This enables us to ``dualize’’ many theorems about concurrency to obtain a theorem about collinearity, or vice versa.
Reciprocation has the added benefit that it preserves conics. One way to define a conic is as the reciprocal of some circle. Alternatively, we can define a conic as the locus of solutions $(a:b:c)$ to some homogeneous equation of degree $2$ in $x,y,z$, such as $x^2+2y^2-z^2=0$ or $x^2-yz=0$.
Exercise. What kind of conics do the two quadratic equations above describe when restricted to the Euclidean plane ($c\neq 0$)?
Projective transformations
In homogeneous coordinates, a \textit{projective transformation} is a map of the form \[(x:y:z)\mapsto (ax+by+cz:dx+ey+fz:gx+hy+iz)\] for some real $a,b,c,d,e,f,g,h,i$. The main facts we need to know about projective transformations are:
- Projective transformations send lines to lines and conics to conics.
- Projective transformations preserve incidence (collinearity and concurrency).
- Projective transformations preserve cross ratios of collinear points. (The cross ratio of four collinear points $A,B,C,D$ is \[(A,B;C,D)=\frac{AC\cdot BD}{AD\cdot BC}.\] Each factor is a directed length according to a fixed orientation of the line.)
- Given four points $A,B,C,D$ in the projective plane, no three collinear, and another such choice of points $X,Y,Z,W$, there is a unique projective transformation sending $A$ to $X$, $B$ to $Y$, $C$ to $Z$, and $D$ to $W$.
It is often useful to choose an important line in a diagram and apply a projective transformation sending that line to the line at infinity.
Some theorems and their duals
We finally have the tools to prove some powerful about Euclidean geometry that are more natural in the context of projective geometry. Can you see why reciprocation sends each theorem to its dual?
| Theorem | Dual |
| Ceva: If $ABC$ is a triangle, cevians $AY, BZ, CX$ concur if and only if $\frac{AX}{XB}\cdot\frac{BY}{YC}\cdot\frac{CZ}{ZA}=1$. | Menelaus: If $ABC$ is a triangle, points $X, Y, Z$ on lines $AB, BC, CA$ respectively are collinear if and only if $\frac{AX}{XB}\cdot\frac{BY}{YC}\cdot\frac{CZ}{ZA}=-1$. |
| Desargues: If $ABC$ and $DEF$ are two triangles, then $AD$, $BE$, and $CF$ are concurrent if and only if $AB\cap DE$, $BC\cap EF$, and $CA\cap FD$ are collinear. | Desargues: If $ABC$ and $DEF$ are two triangles, then $AD$, $BE$, and $CF$ are concurrent if and only if $AB\cap DE$, $BC\cap EF$, and $CA\cap FD$ are collinear. |
| Pascal: Given a hexagon inscribed in a conic, the intersection points of the pairs of opposite sides are collinear. | Brianchon: Given a hexagon circumscribed about a conic, the lines joining the pairs of opposite points are concurrent. |
Let’s illustrate the power of projective transformations by proving Desargues’ Theorem. Let $ABC$ and $DEF$ be triangles and assume $X=AB\cap DE$, $Y=BC\cap EF$, and $Z=CA\cap FD$ are collinear. Consider a projective transformation that sends $X$ and $Y$ to two points $X’$ and $Y’$ on the line at infinity. Since projective transformations preserve incidence, we only need to show that the image of $Z$ under this transformation, $Z’$, is on the line at infinity if and only if the images of the triangles, $A’B’C’$ and $D’E’F’$, have the property that $A’D’$, $B’E’$, and $C’F’$ are concurrent. (In this case we say the triangles are perspective from a point.)
Since $X’=A’B’\cap D’E’$ and $Y’=B’C’\cap E’F’$ and these are both on the line at infinity, we have $A’B’||D’E’$ and $B’C’||E’F’$. So we’ve created parallel lines to work with. Now, if $Z’$ is also on the line at infinity, then the third pair of sides of the triangles, $A’C’$ and $D’F’$, are also parallel, and so the triangles are homothetic (that is, one can be mapped to another via a dilation of the plane centered at some chosen point). The center of this homothety must lie on each of $A’D’$, $B’E’$, and $C’F’$, and so the triangles $A’B’C’$ and $D’E’F’$ are perspective from this point.
Conversely, if $A’D’$, $B’E’$, and $C’F’$ intersect at $P$, then the homothety centered at $P$ sending $B’$ to $E’$ must send $A’$ to $D’$ and $C’$ to $F’$ because of the two pairs of parallel lines. So, the third pair of lines must also be parallel, and so $Z’$ is on the line at infinity.