Glencoe/McGraw-Hill doesn't believe this bijection exists
Education is a difficult task, it really is. Teaching takes a few tries to get the hang of. Writing textbooks is even harder. And math is one of those technical fields in which human error is hard to avoid. So usually, when I see a mistake in a math text, it doesn’t bother me much.
But some things just hurt my soul.
No correspondence between the integers and rationals? Yes there is, Example 2! Yes there is!
This horrifying falsehood was stated in the supplementary ``Study Guide and Intervention’’ worksheet for the Glencoe/McGraw-Hill Algebra 2 textbook, and recently pointed out on Reddit. Or at least it was stated in some version of this worksheet. The original file can be found online at various websites, including one download link from Glencoe’s website that shows up on a Google search. There are other versions of the document that don’t contain this example, but this version was almost certainly used in some high schools, as the Reddit thread claims.
Luckily, mathematicians are here to set the record straight. The Wolfram blog published a fantastic post about this error already, with several proofs of the countability of the rationals. There are also several excellent older expositions on this topic, including on the Math Less Traveled and the Division by Zero blogs. I’ll discuss two of my favorites here as well.
But first, let’s talk about what is wrong with the argument in Example 2. The author is correct in stating that listing all the rationals in order would make a one-to-one and onto correspondence between the rationals and integers, and so they try to do so in a random way and failed. At that point, instead of trying a different ordering, they gave up and figured it couldn’t be done! That’s not a proof, or even logically sound (as my students at this year’s Prove it! Math Academy would certainly recognize.)
If one were going to try to prove that a certain set couldn’t be organized into a list, a common tactic would be to use proof by contradiction: assume there was a way to list them, and then show that something goes wrong and you get a contradiction. Of course, this wouldn’t work either in the case of the rationals, because they can be listed.
So let’s discuss a correct solution.
Getting our definitions straight
First, let’s state the precise meaning of a one-to-one and onto correspondence. A function $f$ from a set $A$ to a set $B$, written $f:A\to B$, is an assignment of each element of $a\in A$ to an element $f(a)\in B$. To clear up another misuse of notation in the Glencoe Algebra textbook, the set $A$ is called the domain and $B$ is called the codomain (not the range, as Glencoe would have you think - the range refers to the set of elements of $B$ that are assigned to by the function.) A function is:
- One-to-one, or injective, if no two elements of $A$ are assigned to the same element of $B$, i.e., if $f(x)=f(y)$ then $x=y$.
- Onto, or surjective, if every element of $B$ is mapped to, i.e., for all $b\in B$, there exists $a\in A$ such that $f(a)=b$.
For instance, if $\mathbb{Z}$ denotes the set of integers, the function $f:\mathbb{Z}\to \mathbb{Z}$ defined by $f(x)=2x$ is injective, since if $2x=2y$ then $x=y$. However, it is not surjective, since an odd number like $3$ is not equal to $2x$ for any integer $x$.
A function which is both injective and surjective is said to be bijective, and is called a bijection. This is just a shorter way of saying ``one-to-one and onto correspondence,’’ which is wordy and cumbersome.
So, we want to find a bijection $f:\mathbb{Z}\to \mathbb{Q}$, where $\mathbb{Z}$ denotes the integers and $\mathbb{Q}$ the rationals. Notice that we can list all the integers in order: \[0,1,-1,2,-2,3,-3,\ldots\] and so if we list all the rationals in order, $r_0,r_1,r_2,\ldots$, we can define the function $f$ accordingly by $f(0)=r_0$, $f(1)=r_1$, $f(-1)=r_2$, and so on. The function will be bijective if and only if every rational number appears in the list exactly once.
Next, let’s be precise about the rationals. Recall that the rational numbers are those numbers which can be written as fractions $a/b$ where $a$ and $b$ are integers with $b\neq 0$. In order to assign every rational number a unique representation, let us restrict to the case where $b>0$ and $a$ is any integer such that $\mathrm{gcd}(a,b)=1$. This condition makes $a/b$ into a reduced fraction. So the number $2/-4$ should be written as $-1/2$ in this convention. It follows that we can think of the set of rational numbers as the set \[\mathbb{Q}=\{(a,b) | b>0\text{ and }\mathrm{gcd}(a,b)=1\text{ and }a,b\in \mathbb{Z}\}.\]
Listing the rationals, naively
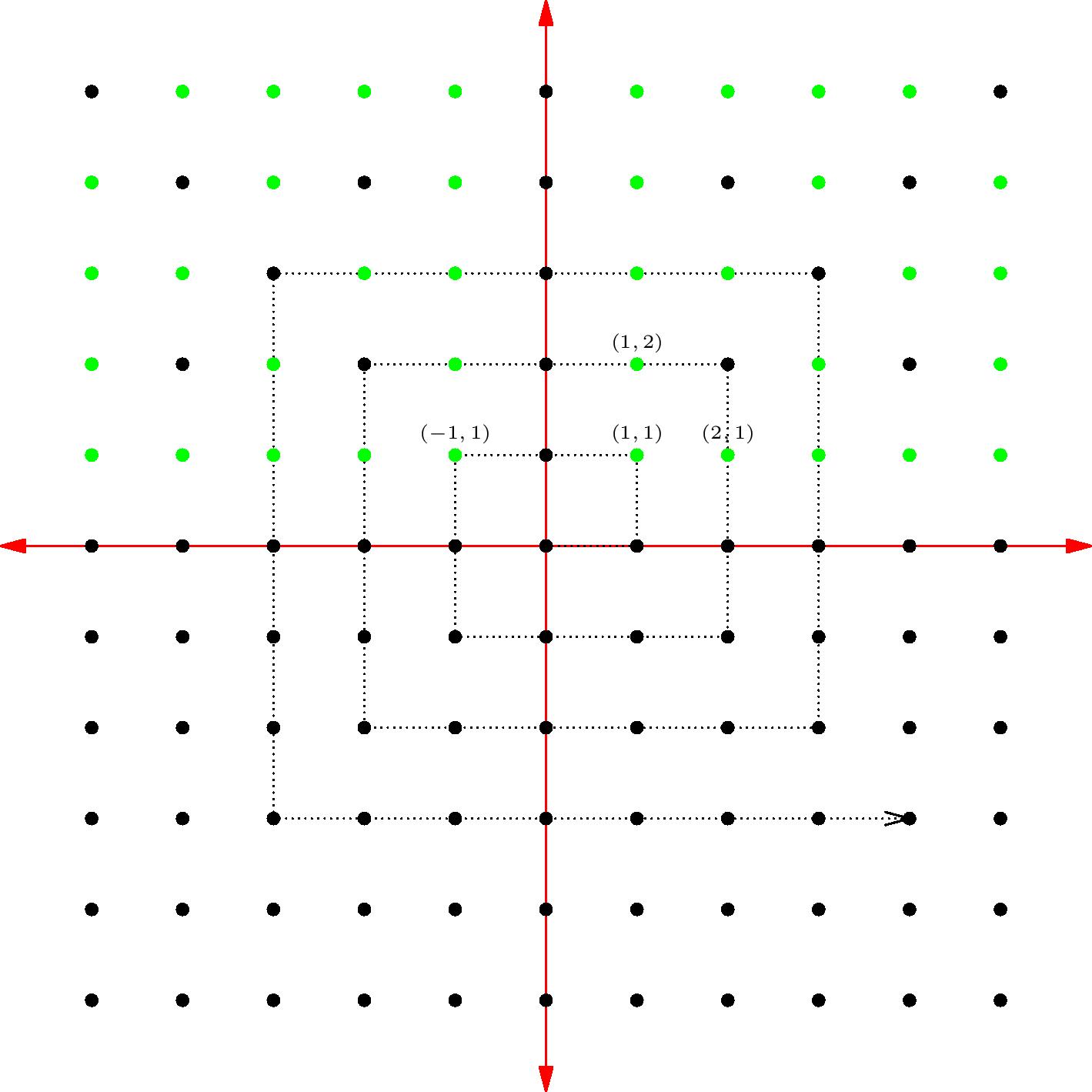
One way to construct this list is to think of the rationals as ordered pairs $(a,b)$ of integers with $b>0$ and $\mathrm{gcd}(a,b)=1$ as described above. There is an easy way of ordering all pairs of integers - plot them on a coordinate plane, and use a spiral!
Now, to list the rationals, follow the spiral from $(0,0)$ outwards. Each time we reach an ordered pair of integers, say $(a,b)$, write it down if $b>0$ and $\mathrm{gcd}(a,b)=1$, and otherwise skip it and move on. (These are the green dots above.) This process guarantees that we list all the rationals exactly once.
More elegant methods
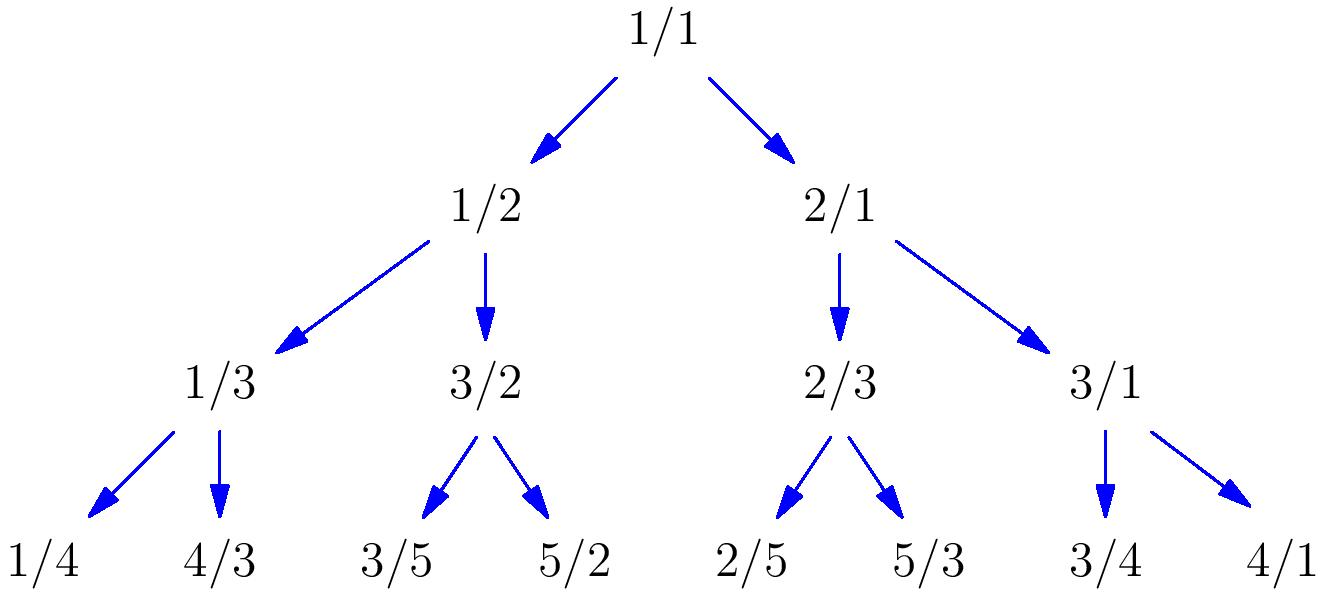
There are many other elegant enumerations of the rationals, and one particularly nice one is due to Calkin and Wilf. They construct a binary tree in which each rational number appears exactly once, as shown below.
The tree is constructed as follows: start with $1/1$ at the top, and for each node $a/b$ in the tree, assign it the left and right children $a/(a+b)$ and $(a+b)/b$ respectively. This tree turns out to contain every positive rational number exactly once. It also has an incredible property: if we read the entries of each row of the tree successively from left to right, the denominator of each entry will match the numerator of the next entry, giving us a sequence of numerators/denominators: \[1,1,2,1,3,2,3,1,4,3,5,2,5,3,4,1,\ldots\] such that the consecutive quotients give us a list of the positive rationals.
This makes me wonder is whether there is a way of listing the integers such that (a) every integer occurs exactly once in the sequence, and (b) the consecutive quotients give all rationals exactly once (allowing the consecutive integers to have common factors greater than one). Thoughts?